1
GATE ECE 2002
MCQ (Single Correct Answer)
+1
-0.3
Convolution of x(t + 5) with impulse function $$\delta \left( {t\, - \,7} \right)$$ is equal to
2
GATE ECE 2002
Subjective
+5
-0
A deterministic signal x(t) = $$\cos (2\pi t)$$ is passed through a differentiator as shown in
Figure.
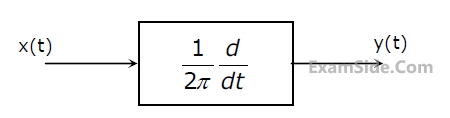
(a) Determine the autocorrelation Rxx ($$\tau $$) and the power spectral density Sxx(f).
(b) Find the output power spectral density Syy( f ).
(c) Evaluate Rxy(0) and Rxy(1/4).
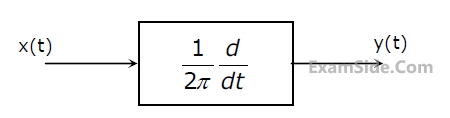
(a) Determine the autocorrelation Rxx ($$\tau $$) and the power spectral density Sxx(f).
(b) Find the output power spectral density Syy( f ).
(c) Evaluate Rxy(0) and Rxy(1/4).
3
GATE ECE 2002
MCQ (Single Correct Answer)
+2
-0.6
If the impulse response of a discrete-time system is $$h\left[ n \right]\, = \, - {5^n}\,\,u\left[ { - n\, - 1} \right],$$ then the system function $$H\left( z \right)\,\,\,$$ is equal to
4
GATE ECE 2002
MCQ (Single Correct Answer)
+1
-0.3
Consider a sampled signal $$y\left( t \right) = 5 \times {10^{ - 6}}\,x\left( t \right)\,\,\sum\limits_{n = - \infty }^{ + \infty } {\delta \left( {t - n{T_s}} \right)} $$
where $$x\left( t \right) = 10\,\,\cos \,\left( {8\pi \times {{10}^3}} \right)\,\,t$$ and
$${T_s} = 100\,\,\mu \sec .$$ When $$y\left( t \right)$$ is passed through an ideal low-pass filter with a cutoff frequency of 5 KHz, the output of the filter is
Paper analysis
Total Questions
Analog Circuits
4
Communications
3
Control Systems
11
Digital Circuits
7
Electromagnetics
11
Electronic Devices and VLSI
4
Microprocessors
2
Network Theory
8
Signals and Systems
10
More papers of GATE ECE
GATE ECE 2025
GATE ECE 2024
GATE ECE 2023
GATE ECE 2022
GATE ECE 2021
GATE ECE 2019
GATE ECE 2018
GATE ECE 2017 Set 2
GATE ECE 2017 Set 1
GATE ECE 2016 Set 3
GATE ECE 2016 Set 2
GATE ECE 2016 Set 1
GATE ECE 2015 Set 2
GATE ECE 2015 Set 3
GATE ECE 2015 Set 1
GATE ECE 2014 Set 1
GATE ECE 2014 Set 4
GATE ECE 2014 Set 3
GATE ECE 2014 Set 2
GATE ECE 2013
GATE ECE 2012
GATE ECE 2011
GATE ECE 2010
GATE ECE 2009
GATE ECE 2008
GATE ECE 2007
GATE ECE 2006
GATE ECE 2005
GATE ECE 2004
GATE ECE 2003
GATE ECE 2002
GATE ECE 2001
GATE ECE 2000
GATE ECE 1999
GATE ECE 1998
GATE ECE 1997
GATE ECE 1996
GATE ECE 1995
GATE ECE 1994
GATE ECE 1993
GATE ECE 1992
GATE ECE 1991
GATE ECE 1990
GATE ECE 1989
GATE ECE 1988
GATE ECE 1987
GATE ECE
Papers
2025
2024
2023
2022
2021
2019
2018
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987