1
GATE EE 2006
MCQ (Single Correct Answer)
+2
-0.6
$$y\left[ n \right]$$ denotes the output and $$x\left[ n \right]$$ denotes the input of a discrete-time system given by the difference equation $$y\left[ n \right] - 0.8y\left[ {n - 1} \right] = x\left[ n \right] + 1.25\,x\left[ {n + 1} \right].$$ Its right-sided impulse response is
2
GATE EE 2004
MCQ (Single Correct Answer)
+2
-0.6
In the system shown in Fig. the input $$x\left( t \right) = \sin t.$$ In the steady-state, the response $$y(t)$$ will be
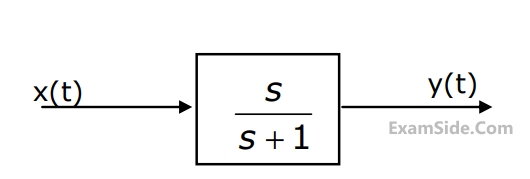

3
GATE EE 2001
MCQ (Single Correct Answer)
+2
-0.6
Given the relationship between the input $$u(t)$$ and the output $$y(t)$$ to be
$$y\left( t \right) = \int\limits_0^t {\left( {2 + t - \tau } \right){e^{ - 3\left( {t - \tau } \right)}}} u\left( \tau \right)d\tau $$
the transfer function $$Y\left( s \right)/U\left( s \right)$$ is
$$y\left( t \right) = \int\limits_0^t {\left( {2 + t - \tau } \right){e^{ - 3\left( {t - \tau } \right)}}} u\left( \tau \right)d\tau $$
the transfer function $$Y\left( s \right)/U\left( s \right)$$ is
Questions Asked from Linear Time Invariant Systems (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electric Circuits
Electromagnetic Fields
Signals and Systems
Electrical Machines
Engineering Mathematics
General Aptitude
Power System Analysis
Electrical and Electronics Measurement
Analog Electronics
Control Systems
Power Electronics