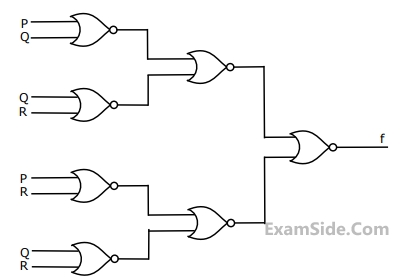
What is the Boolean expression for the output f of the combinational logic circuit of NOR gates given below?

If $$P, Q, R$$ are Boolean variables, then $$\left( {P + \overline Q } \right)$$ $$\left( {P.\overline Q + P.R} \right)\left( {\overline P .\overline R + \overline Q } \right)$$ Simplifies to

Let $$f\left( {w,x,y,z} \right) = \sum {\left( {0,4,5,7,8,9,13,15} \right).} $$ Which of the following expressions are NOT equivalent to $$f?$$
$$(P)\,\,\,$$ $$x'y'z' + w'xy' + wy'z + xz$$
$$(Q)\,\,\,$$ $$w'y'z' + wx'y' + xz$$
$$(R)\,\,\,$$ $$w'y'z' + wx'y' + xyz + xy'z$$
$$(S)\,\,\,$$ $$x'y'z' + wx'y' + w'y$$

Consider a Boolean function $$f(w, x, y, z).$$ Suppose that exactly one of its inputs is allowed to change at a time. If the function happens to be true for two input vectors $${i_1} = < {w_1},{x_1},{y_1},{z_1} > $$ and $${i_2} = < {w_2},{x_2},{y_2},{z_2} > ,$$ we would like the function to remain true as the input changes from $${i_1}$$ to $${i_2}$$ ($${i_1}$$ and $${i_2}$$ differ in exactly one bit position), without becoming false momentarily. Let $$f\left( {w,x,y,z} \right) = \sum {\left( {5,7,11,12,13,15} \right)} .$$ Which of the following cube covers of $$f$$ will entire that the required property is satisfied?