1
GATE EE 2002
Subjective
+5
-0
Two transposed $$3$$ phase lines run parallel to each other. The equation describing the voltage drop in both lines is given below.
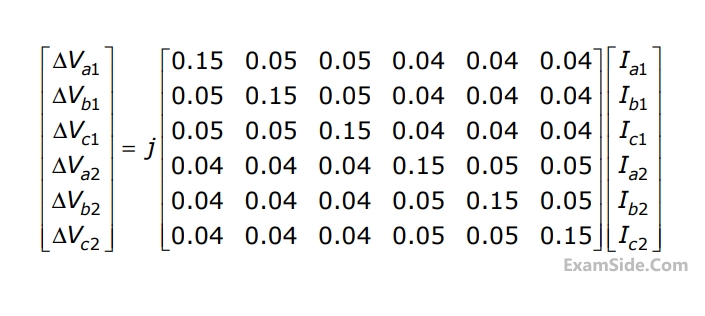

Compute the self and mutual zero sequence impedances of this system i.e, compute $${Z_{011}},\,\,{Z_{012}},\,\,{Z_{021}},\,\,{Z_{022}}\,\,\,$$ in the following equations.
$$\Delta {V_{01}} = {Z_{011}}\,{{\rm I}_{01}} + {Z_{012}}\,{{\rm I}_{02}}$$
$$\Delta {V_{02}} = {Z_{021}}\,{{\rm I}_{01}} + {Z_{022}}\,{{\rm I}_{02}}\,\,$$ where $$\,\Delta {V_{01}},$$
$$\Delta {V_{02}},\,{{\rm I}_{01}},\,{{\rm I}_{02}}\,\,$$ are the zero sequence voltage drops and currents for the two lines respectively.
2
GATE EE 2001
Subjective
+5
-0
For the $$Y$$-$$bus$$ matrix given in per unit values, where the first, second, third and fourth row refers to bus $$1, 2, 3$$ and $$4$$ respectively, draw the reactance diagram.
$$${Y_{bus}} = j\left[ {\matrix{
{ - 6} & 2 & {2.5} & 0 \cr
2 & { - 10} & {2.5} & 4 \cr
{2.5} & {2.5} & { - 9} & 4 \cr
0 & 4 & {4 - 8} & {} \cr
} } \right]$$$
Questions Asked from Load Flow Studies (Marks 5)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electric Circuits
Electromagnetic Fields
Signals and Systems
Electrical Machines
Engineering Mathematics
General Aptitude
Power System Analysis
Electrical and Electronics Measurement
Analog Electronics
Control Systems
Power Electronics