The velocity profile across a boundary layer on a flat plate may be approximated as linear $$${V_x}\left( {x,y} \right) = {{{V_0}y} \over {\delta \left( x \right)}}$$$

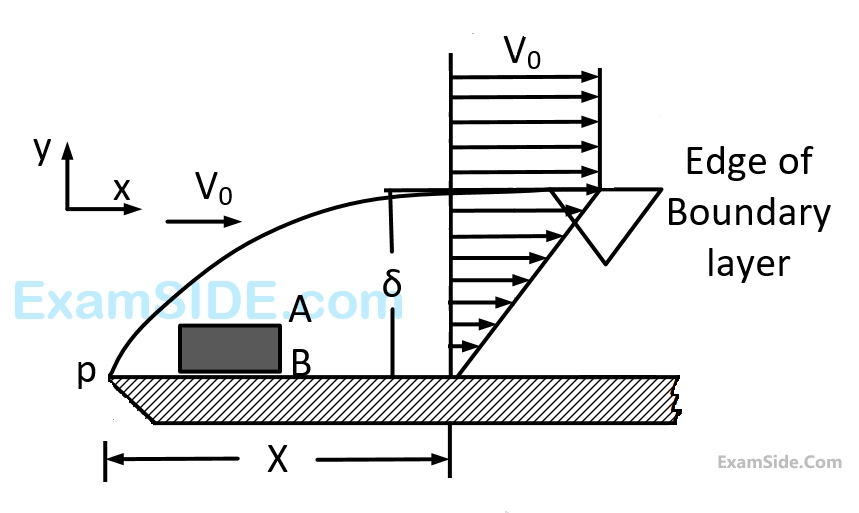
Where $${{V_0}}$$ is the velocity far away and $$\delta \left( x \right)$$ is the boundary layer thickness at a distance $$x$$ from the leading edge, as shown below.

(a)$$\,\,\,\,\,\,$$ Use an appropriate control volume to determine the rate of mass influx into the
$$\,\,\,\,\,\,$$$$\,\,$$$$\,\,\,\,\,\,$$boundary layer up to $$x.$$

(b)$$\,\,\,\,\,\,$$ Obtain the momentum thickness into the boundary layer up to $$x.$$

(c)$$\,\,\,\,\,\,$$ In which direction (up or down) does the shear stress act on the face $$AB$$ of
$$\,\,\,\,\,\,$$$$\,\,\,\,\,\,\,$$the fluid element shown near the plate?