1
GATE EE 2015 Set 2
MCQ (Single Correct Answer)
+2
-0.6
The unit step response of a system with the transfer function $$G\left( s \right) = {{1 - 2s} \over {1 + s}}$$ is given by which one of the following waveforms?
2
GATE EE 2013
MCQ (Single Correct Answer)
+2
-0.6
The open-loop transfer function of a $$dc$$ motor is given as $${{\omega \left( s \right)} \over {{V_a}\left( s \right)}} = {{10} \over {1 + 10s}}.$$ When connected in feedback as shown below, the approximate value of $${K_a}$$ that will reduce the time constant of the closed loop system by one hundred times as compared to that of the open-loop system is
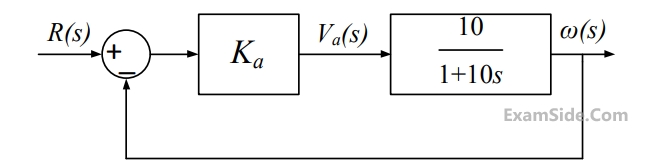

3
GATE EE 2011
MCQ (Single Correct Answer)
+2
-0.6
A two-loop position control system is shown below.
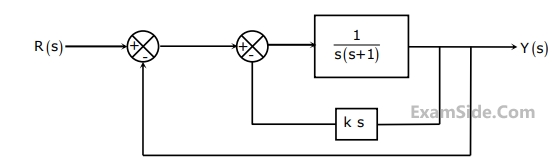
The gain $$k$$ of the Tacho-generator influences mainly the

The gain $$k$$ of the Tacho-generator influences mainly the
4
GATE EE 2011
MCQ (Single Correct Answer)
+2
-0.6
The response $$h(t)$$ of a linear time invariant system to an impulse $$\delta \left( t \right),$$ under initially relaxed condition is $$h\left( t \right) = \,{e^{ - t}} + {e^{ - 2t}}.$$ The response of this system for a unit step input $$u(t)$$ is
Questions Asked from Time Response Analysis (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electromagnetic Fields
Signals and Systems
Engineering Mathematics
General Aptitude
Power Electronics
Power System Analysis
Analog Electronics
Control Systems
Digital Electronics
Electrical Machines
Electric Circuits



