Let $f(.)$ be a twice differentiable function from $ \mathbb{R}^{2} \rightarrow \mathbb{R}$. If $P, \mathbf{x}_{0} \in \mathbb{R}^{2}$ where $\vert \vert P\vert \vert$ is sufficiently small (here $\vert \vert . \vert \vert$ is the Euclidean norm or distance function), then $f (\mathbf{x}_{0} + p) = f(\mathbf{x}_{0}) + \nabla f(\mathbf{x}_{0})^{T}p + \dfrac{1}{2} p^{T} \nabla^{2}f(\psi)p$ where $\psi \in \mathbb{R}^{2}$ is a point on the line segment joining $\mathbf{x}_{0}$ and $\mathbf{x}_{0} + p$. If $\mathbf{x}_{0}$ is a strict local minimum of $f (\mathbf{x})$, then which one of the following statements is TRUE?
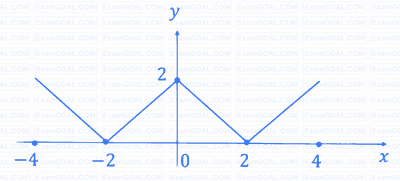
The figure shows the plot of a function over the interval [-4, 4]. Which one of the options given CORRECTLY identifies the function?
Given $\int^{\infty}_{-\infty}e^{-x^2}dx=\sqrt{\pi}$
If a and b are positive integers, the value of $\int^{\infty}_{-\infty}e^{-a(x+b)^2}dx$ is _________.