A control system with certain excitation is governed by the following mathematical equation
$$${{{d^2}x} \over {d{t^2}}} + {1 \over 2}{{dx} \over {dt}} + {1 \over {18}}x = 10 + 5{e^{ - 4t}} + 2{e^{ - 5t}}$$$
The natural time constants of the response of the system are
A
$$2s$$ and $$5s$$
B
$$3s$$ and $$6s$$
C
$$4s$$ and $$5s$$
D
$$1/3s$$ and $$1/6s$$
2
GATE EE 2003
MCQ (Single Correct Answer)
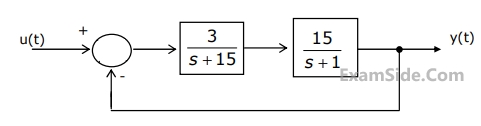
The roots of the closed loop characteristic equation of the system shown in fig is
A
$$-1$$ and $$-15$$
B
$$6$$ and $$10$$
C
$$-4$$ and $$-15$$
D
$$-6$$ and $$-10$$
3
GATE EE 2003
MCQ (Single Correct Answer)
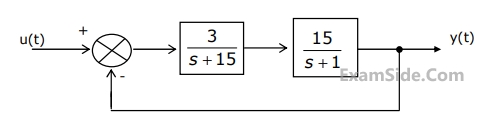
The block diagram shown in fig given is a unity feedback closed loop control system. The steady state error in the response of the above system to unit step input is
A
$$25\% $$
B
$$0.75\% $$
C
$$6\% $$
D
$$33\% $$
4
GATE EE 2000
MCQ (Single Correct Answer)
A unity feedback system has open-loop transfer function $$G\left( s \right) = {{25} \over {s\left( {s + 6} \right)}}.$$ The peak overshoot in the step-input response of the system is approximately equal to
A
$$5\% $$
B
$$10\% $$
C
$$15\% $$
D
$$20\% $$
Write for Us
Do you want to write for us? Help us by contributing to our platform.
