For the circuit in Fig.

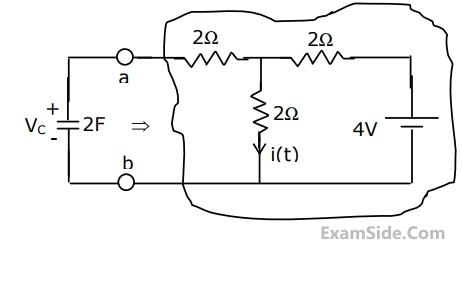
(a) Find the Thevenin equivalent of the sub circuit faced by the capacitor across the terminals a, b.

(b) Find $$v_c\left(t\right),\;t>0,\;given\;v_c(0)\;=\;0.$$

(c) Find i(t), t>0.

In the circuit of Fig., the votage v(t) is

Given that $$L\left[ {f\left( t \right)} \right]\, = \,$$ $${{s + 2} \over {{s^2} + 1}},$$ $$$L\left[ {g\left( t \right)} \right] = {{{s^2} + 1} \over {\left( {s + 3} \right)\left( {s + 2} \right)}},$$$ $$$h\left( t \right) = \int\limits_0^t {f\left( \tau \right)\,g\left( {t - \tau } \right)\,d\tau ,} $$$ $$L\left[ {h\left( t \right)} \right]$$ is

A system with an input x(t) and an output y(t) is described by the relation: y(t) = t x(t). This system is