A plane wave in free space with
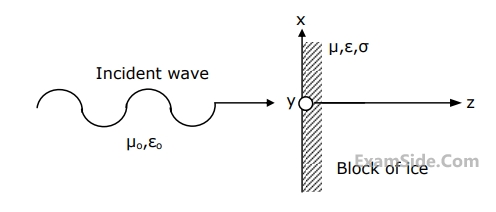
$$\overrightarrow E = \left( {\sqrt \pi } \right)\left( {10.0\,\widehat x + 11.8\,\widehat y} \right)\exp \left[ {j\left( {4\pi \times {{10}^8}\,t - k\,z} \right)} \right]$$
where $$\widehat x$$ and $$\widehat y$$ are unit vectors in the $$x$$- and $$y$$-directions respectively is incident normally on a semi-infinite block of ice as shown in Fig. For ice, $$\mu = {\mu _0},\,\,\,\sigma = 0$$ and $$\varepsilon = 9{\varepsilon _0}\left( {1 - j0.001} \right)$$.

(a) Calculate the average power density associated with the incident wave.

(b) Calculate the skin depth in ice.

(c) Estimate the average power density at a distance of 5 times the skins depth in the ice block, measured from the interface.

A transmitting antenna radiates 251 W isotropically. A receiving antenna, located 100m away from the transmitting antenna, has an effective aperture of 500 cm². The total power received by the antenna is

The average power of an omni-directional antenna varies as the magnitude of cos($$\theta $$) where $$\theta $$ is the azimuthal angle. Calculate the maximum Directive Gain of the antenna and the angles at which it occurs.

A 100 m section of an air-filled rectangular wave-guide operating in the $$T{E_{10}}$$ mode has a cross-sectional dimension of 1.071 cm $$ \times $$ 0.5 cm. Two pulses carriers of 21 GHz and 28 GHz are simultaneously launched at one end of the wave-guide section. What is the time delay difference between the two pulses at the other end of the waveguide?