ExamSIDE (Powered by ExamGOAL)
Questions
PREVIOUS NEXT
1
GATE EE 2013
MCQ (Single Correct Answer)
+1
-0.3
The impulse response of a system is h(t) = tu(t). For an input u(t − 1), the output is
A
$$\frac{t^2}2u\left(t\right)$$
B
$$\frac{t\left(t-1\right)}2u\left(t-1\right)$$
C
$$\frac{\left(t-1\right)^2}2u\left(t-1\right)$$
D
$$\frac{t^2-1}2u\left(t-1\right)$$
2
GATE EE 2013
MCQ (Single Correct Answer)
+1
-0.3
Two systems with impulse responses h1(t) and h2(t) are connected in cascade. Then the overall impulse response of the cascaded system is given by
A
product of h1(t) and h2(t)
B
Sum of h1(t) and h2(t)
C
Convolution of h1(t) and h2(t)
D
subtraction of h2(t) and h1(t)
3
GATE EE 2013
MCQ (Single Correct Answer)
+1
-0.3
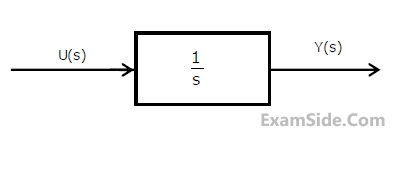
Assuming zero initial condition, the response y(t) of the system given below to a unit step input u(t) is GATE EE 2013 Signals and Systems - Linear Time Invariant Systems Question 45 English
A
u(t)
B
tu(t)
C
$$\frac{t^2}2u\left(t\right)$$
D
$$e^{-t}u\left(t\right)$$
4
GATE EE 2011
MCQ (Single Correct Answer)
+1
-0.3
A low–pass filter with a cut-off frequency of 30 Hz is cascaded with a high-pass filter with a cut-off frequency of 20 Hz. The resultant system of filters will function as
A
an all-pass filter
B
an all-stop filter
C
an band stop (band-reject) filter
D
a band–pass filter
PREVIOUS NEXT
GATE EE Subjects
Electric Circuits
Network Elements Network Theorems Three Phase Circuits Transient Response Sinusoidal Steady State Analysis Graph Theory Two Port Networks
Electromagnetic Fields
Time Varying Fields Electrostatics Magnetostatics
Signals and Systems
Continuous and Discrete Time Signals Linear Time Invariant Systems Continuous Time Signal Fourier Transform Discrete Time Signal Z Transformation Continuous Time Signal Laplace Transform Sampling Theorem Continuous Time Periodic Signal Fourier Series Miscellaneous
Electrical Machines
Induction Machines D.C Machines Synchronous Machines Transformers
Engineering Mathematics
Calculus Vector Calculus Linear Algebra Differential Equations Probability and Statistics Transform Theory Complex Variable Numerical Methods
General Aptitude
Verbal Ability Logical Reasoning Numerical Ability
Power System Analysis
Parameters and Performance of Transmission Lines Power Generation Cost Power System Stability Symmetrical Components and Symmetrical and Unsymmetrical Faults Circuit Breaker Switch Gear and Protection Per Unit System Load Flow Studies High Voltage Dc Transmission Generating Power Station
Electrical and Electronics Measurement
Error Analysis and Measurement Basic of Indicating Instruments Potentiometer and Instrument Transformers Measurement of Resistance and A.C Bridges Measurement of Energy and Power Digital Voltmeters Questions Cathode Ray Oscilloscope
Analog Electronics
Diode Circuits and Applications Bjt and Mosfet Biasing Small Signal Modeling Feedback Amplifiers and Oscillator Circuits Operational Amplifier Frequency Response 555 Timer
Control Systems
Block Diagram and Signal Flow Graph Polar Nyquist and Bode Plot State Variable Analysis Basics of Control System Routh Hurwitz Stability Time Response Analysis Root Locus Techniques Controller and Compensator
Power Electronics
Choppers and Commutation Techniques Ac Voltage Controllers Single and Three Phase Rectifier Power Semiconductor Devices Inverters
Digital Electronics
Boolean Algebra Logic Gates Combinational Circuits Minimization Logic Families and Memories Sequential Circuits Analog to Digital and Digital to Analog Converter Microprocessor
EXAM MAP
Joint Entrance Examination
JEE MainJEE AdvancedWB JEEBITSATMHT CETKCETCOMEDKVITEEEAP EAPCET
Medical
NEETAIIMS
Graduate Aptitude Test in Engineering
GATE CSEGATE ECEGATE EEGATE MEGATE CEGATE PIGATE IN
Civil Services
UPSC Civil Service
Defence
NDA
Staff Selection Commission
SSC CGL Tier I
CBSE
Class 12