The following is a scheme for floating point number representation using $$16$$ bits.

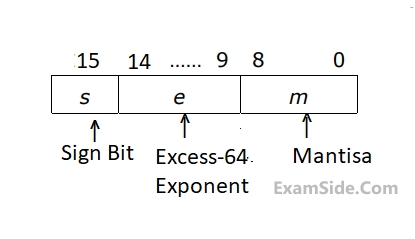
Let $$s, e,$$ and $$m$$ be the numbers represented in binary in the sign, exponent, and mantissa fields respectively. Then the floating point number represented is

$$\left\{ {\matrix{ {{{\left( { - 1} \right)}^s}\left( {1 + m \times {2^{ - 9}}} \right){2^{e - 31}},} & {if\,the\,{\mathop{\rm exponent}\nolimits} \, \ne \,111111} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0} & {otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \cr } } \right.$$

What is the maximum difference between two successive real numbers representable in this system?

Sign extension is the step in

Booth’s coding in $$8$$ bits for the decimal number –$$57$$ is:

The number of full and half-adders required to add 16-bit numbers is: