The data given below. Solve the problems and choose the correct answer.

Mantissa is a pure fraction in sign - magnitude form. The decimal number $$0.239 \times {2^{13}}$$ has the following hexadecimal representation without normalization and rounding off

The data given below. Solve the problems and choose the correct answer.

The normalized representation for the above format is specified as follows. The mantissa has an implicit preceding the binary (radix) point. Assume that only $$0's$$ are padded in while shifting a field. The normalized representation of the above $$\left( {0.239 \times {2^{13}}} \right)$$ is

$$A$$ $$4$$-bit carry look ahead adder, which adds two $$4$$-bit numbers, is designed using $$AND,$$ $$OR,$$ $$NOT,$$ $$NAND,$$ $$NOR$$ gates only. Assuming that all the inputs are available in both complemented and uncomplemented forms and the delay of each gate is one time unit, what is the overall propagation delay of the adder? Assume that the carry network has been implemented using two-level $$AND$$-$$OR$$ logic.

The following is a scheme for floating point number representation using $$16$$ bits.

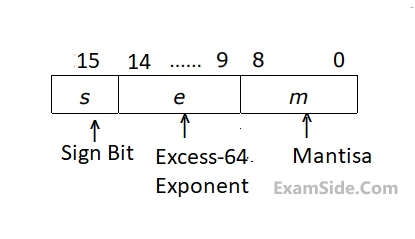
Let $$s, e,$$ and $$m$$ be the numbers represented in binary in the sign, exponent, and mantissa fields respectively. Then the floating point number represented is

$$\left\{ {\matrix{ {{{\left( { - 1} \right)}^s}\left( {1 + m \times {2^{ - 9}}} \right){2^{e - 31}},} & {if\,the\,{\mathop{\rm exponent}\nolimits} \, \ne \,111111} \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0} & {otherwise\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \cr } } \right.$$

What is the maximum difference between two successive real numbers representable in this system?