For the signals $$x(t)$$ and $$y(t)$$ shown in the figure, $$z(t)=x(t)*y(t)$$ is maximum at $$t=T_1$$. Then $$T_1$$ in seconds is __________ (Round off to the nearest integer)

Consider a continuous-time system with input x(t) and output y(t) given by $$y\left(t\right)=x\left(t\right)\cos\left(t\right)$$. This system is

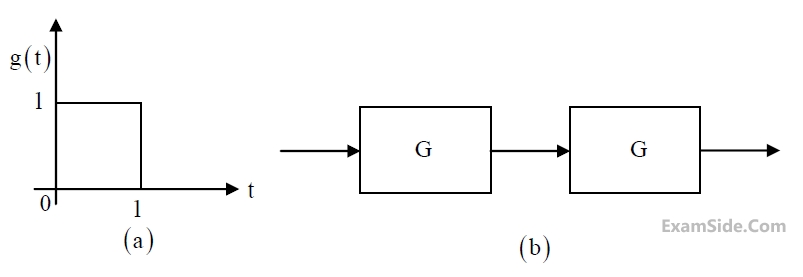
The impulse response g(t) of a system G, is as shown in Figure (a). What is the maximum value attained by the impulse response of two cascaded blocks of G as shown in Figure (b)?

Consider an LTI system with impulse response $$h\left(t\right)=e^{-5t}u\left(t\right)$$ . If the output of the system is $$y\left(t\right)=e^{-3t}u\left(t\right)-e^{-5t}u\left(t\right)$$ then the input, x(t), is given by