Consider two relations describing teams and players in a sports league:
$\bullet$ teams(tid, tname): tid, tname are team-id and team-name, respectively.
$\bullet$ players(pid, pname, tid): pid, pname, and tid denote player-id, player-name and the team-id of the player, respectively.
Which ONE of the following tuple relational calculus queries returns the name of the players who play for the team having tname as ' $M I$ '?
The relation schema, Person($\underline{\text{pid}}$, $city$), describes the city of residence for every person uniquely identified by $pid$. The following relational algebra operators are available: selection, projection, cross product, and rename.
To find the list of cities where at least 3 persons reside, using the above operators, the minimum number of cross product operations that must be used is
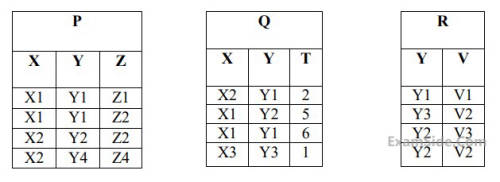
How many tuples will be returned by the following relational algebra query?
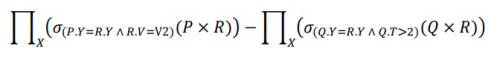
$$Q:$$ $$\,\,\,\,\,\,\,\,\,$$ $$r$$ $$\,\,\,\,$$ $$\bowtie$$ $$\,\,\,\,$$ $$\left( {{\sigma _{b < 5}}\left( s \right)} \right)$$
Let $$LOJ$$ denote the natural left outer-join operation. Assume that $$r$$ and $$s$$ contain no null values.
Which one of the following queries is NOT equivalent to $$Q$$?