Open-loop transfer function of a unity - feedback system is $$$G\left( s \right) = {G_1}\left( s \right).{e^{ - s{\tau _D}}} = {{{e^{ - s{\tau _D}}}} \over {s\left( {s + 1} \right)\left( {s + 2} \right)}}$$$
Given : $$\,\left| {{G_1}\left( {j\omega } \right)} \right| \approx 1$$ when $$\omega = 0.446$$

(a) Determine the phase margin when $${\tau _D} = 0$$
(b) Comment in one sentence on the effect of dead time on the stability of the system.
(c) Determine the maximum value of dead time $${\tau _D}$$ for the closed-loop system to be stable.

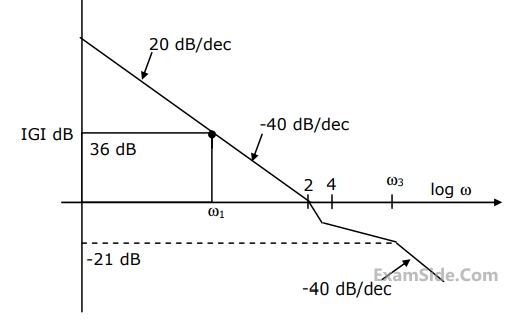
The asymptotic magnitude Body plot of a system is given in Figure. Find the transfer function of the system analytically. It is known that the system is minimal phase system.