1
GATE CSE 2016 Set 2
MCQ (Single Correct Answer)
+1
-0.3
Let, $${x_1} \oplus {x_2} \oplus {x_3} \oplus {x_4} = 0$$ where $${x_1},\,{x_2},\,{x_3},\,{x_4}$$ are Boolean Variables, and $$ \oplus $$ is the $$XOR$$ operator.
Which one of the following must always be TRUE?
2
GATE CSE 2016 Set 1
MCQ (Single Correct Answer)
+1
-0.3
Consider the Boolean operator $$ \ne $$ with the following properties:
$$x \ne 0 = x,\,\,x \ne 1 = \overline x ,\,\,x \ne x = 0$$ and $$x \ne \overline x = 1.$$ Then $$x \ne y$$ is equivalent to
$$x \ne 0 = x,\,\,x \ne 1 = \overline x ,\,\,x \ne x = 0$$ and $$x \ne \overline x = 1.$$ Then $$x \ne y$$ is equivalent to
3
GATE CSE 2015 Set 3
MCQ (Single Correct Answer)
+1
-0.3
Let $$ \ne $$ be a binary operator defined as $$X \ne Y = X' + Y'$$ where $$𝑋$$ and $$𝑌$$ are Boolean variables. Consider the following two statements.
$$$\eqalign{
& \left( {S1} \right)\,\,\,\,\,\,\,\left( {P \ne Q} \right) \ne R = P \ne \left( {Q \ne R} \right) \cr
& \left( {S2} \right)\,\,\,\,\,\,\,Q \ne R = R \ne Q \cr} $$$
Which of the following is/are true for the Boolean variables $$𝑃, 𝑄$$ and $$𝑅$$?
4
GATE CSE 2014 Set 3
MCQ (Single Correct Answer)
+1
-0.3
Consider the following combinational function block involving four Boolean variables $$x, y, a,$$
$$b$$ where $$x, a, b$$ are inputs and $$y$$ is the output.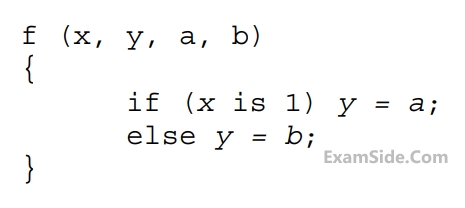
Which one of the following digital logic blocks is the most suitable for implementing this function?
$$b$$ where $$x, a, b$$ are inputs and $$y$$ is the output.
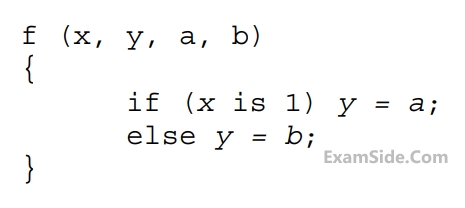
Which one of the following digital logic blocks is the most suitable for implementing this function?
Questions Asked from Boolean Algebra (Marks 1)
Number in Brackets after Paper Indicates No. of Questions
GATE CSE 2025 Set 2 (1)
GATE CSE 2025 Set 1 (1)
GATE CSE 2024 Set 2 (1)
GATE CSE 2019 (1)
GATE CSE 2016 Set 2 (1)
GATE CSE 2016 Set 1 (1)
GATE CSE 2015 Set 3 (1)
GATE CSE 2014 Set 3 (1)
GATE CSE 2014 Set 2 (1)
GATE CSE 2014 Set 1 (1)
GATE CSE 2013 (1)
GATE CSE 2011 (2)
GATE CSE 2010 (1)
GATE CSE 2009 (1)
GATE CSE 2008 (1)
GATE CSE 2007 (1)
GATE CSE 2004 (1)
GATE CSE 1997 (1)
GATE CSE Subjects
Theory of Computation
Operating Systems
Algorithms
Database Management System
Data Structures
Computer Networks
Software Engineering
Compiler Design
Web Technologies
General Aptitude
Discrete Mathematics
Programming Languages