1
GATE EE 2025
Numerical
+2
-0
Let $C$ be a clockwise oriented closed curve in the complex plane defined by $|\lambda|=1$. Further, let $f(x)=j z$ be a complex function, where $j=\sqrt{-1}$. Then, $\oint_C f(z) d z=$ ___________ .
Your input ____
2
GATE EE 2021
MCQ (Single Correct Answer)
+2
-0.67
Let $(-1-j),(3-j),(3+j)$ and $(-1+j)$ be the vertices of rectangle $C$ in the complex plane. Assuming that $C$ is traversed in counter-clockwise direction, the value of contour integral $\oint_C \frac{d z}{z^2(z-4)}$ is
3
GATE EE 2017 Set 2
MCQ (Single Correct Answer)
+2
-0.6
The value of the contour integral in the complex - plane $$\oint {{{{z^3} - 2z + 3} \over {z - 2}}} dz$$ along the contour $$\left| z \right| = 3,$$ taken counter-clockwise is
4
GATE EE 2017 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Consider the line integral $${\rm I} = \int\limits_c {\left( {{x^2} + i{y^2}} \right)dz,} $$ where $$z=x+iy.$$ The line $$c$$ is shown in the figure below.
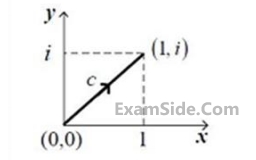
The value of $${\rm I}$$ is
GATE EE Subjects
Browse all chapters by subject
Electric Circuits
Electromagnetic Fields
Signals and Systems
Electrical Machines
Engineering Mathematics
General Aptitude
Power System Analysis
Electrical and Electronics Measurement
Analog Electronics
Control Systems
Power Electronics