1
GATE EE 2012
MCQ (Single Correct Answer)
+1
-0.3
In the circuit shown below, the current through the inductor is


2
GATE EE 2011
MCQ (Single Correct Answer)
+1
-0.3
In the circuit given below, the value of R required for the transfer of maximum
power to the load having a resistance of 3 Ω is


3
GATE EE 2006
MCQ (Single Correct Answer)
+1
-0.3
In the figure the current source is $$1\,\,\angle \,0\,A,$$ $$R = \,1\,\,\Omega ,$$ the impedances are $${Z_C} = - j\,\,\Omega ,$$ and $${Z_L} = 2\,j\,\,\Omega .$$ The Thevenin equivalent looking into the circuit across $$X-Y$$ is.
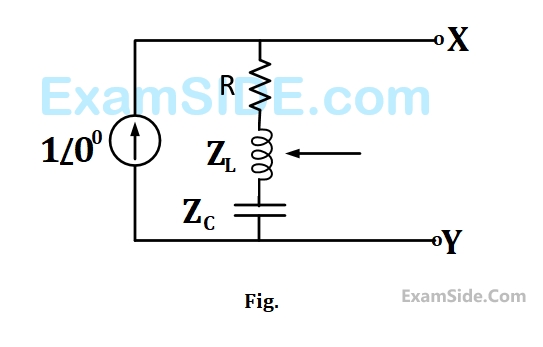

4
GATE EE 2003
MCQ (Single Correct Answer)
+1
-0.3
In the Fig. $${Z_1} = 10\angle - {60^ \circ },\,\,{Z_2} = 10\angle {60^ \circ },\,$$ $${Z_3} = 50\angle {53.13^ \circ }.\,\,$$ Thevenin's impedance seen from $$X-Y$$ is


Questions Asked from Network Theorems (Marks 1)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electric Circuits
Electromagnetic Fields
Signals and Systems
Electrical Machines
Engineering Mathematics
General Aptitude
Power System Analysis
Electrical and Electronics Measurement
Analog Electronics
Control Systems
Power Electronics