1
GATE EE 2002
Subjective
+5
-0
An electrical network is fed by two $$ac$$ sources, as shown in Fig. Given that
$${Z_1} = \left( {1 - j} \right)\Omega ,\,\,{Z_2} = \left( {1 + j} \right)\Omega $$ and $${Z_L} = \left( {1 + j0} \right)\Omega .$$ Obtain the Thevenin equivalent circuit (Thevenin voltage and impedance) across terminals $$X$$ and $$Y$$, and determine the current $${{\rm I}_L}$$ through the load $${Z_L}.$$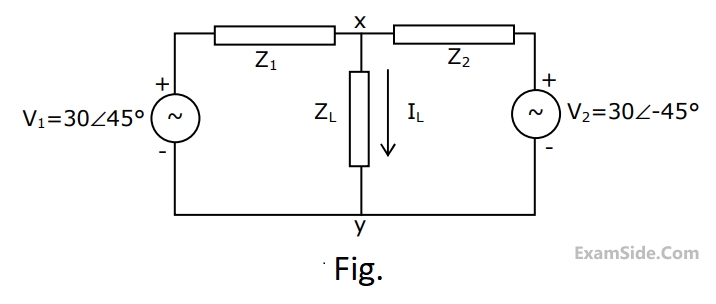
$${Z_1} = \left( {1 - j} \right)\Omega ,\,\,{Z_2} = \left( {1 + j} \right)\Omega $$ and $${Z_L} = \left( {1 + j0} \right)\Omega .$$ Obtain the Thevenin equivalent circuit (Thevenin voltage and impedance) across terminals $$X$$ and $$Y$$, and determine the current $${{\rm I}_L}$$ through the load $${Z_L}.$$

2
GATE EE 2000
Subjective
+5
-0
Predict the current $${\rm I}$$ in Fig. in response to a voltage of $$20\angle {0^0}\,V.$$ The impedance values are given in $$ohms.$$ Use Thevenin's theorem.
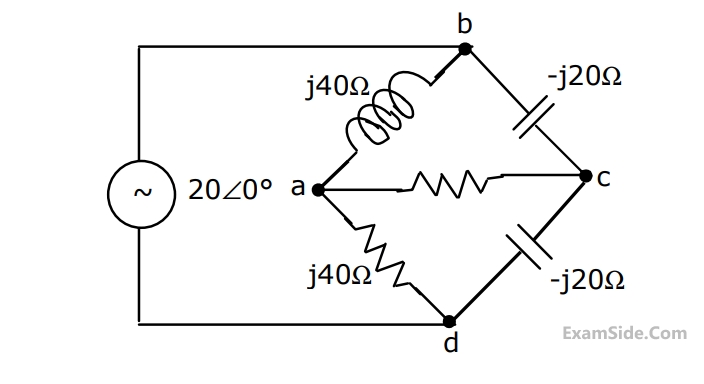

3
GATE EE 1997
Subjective
+5
-0
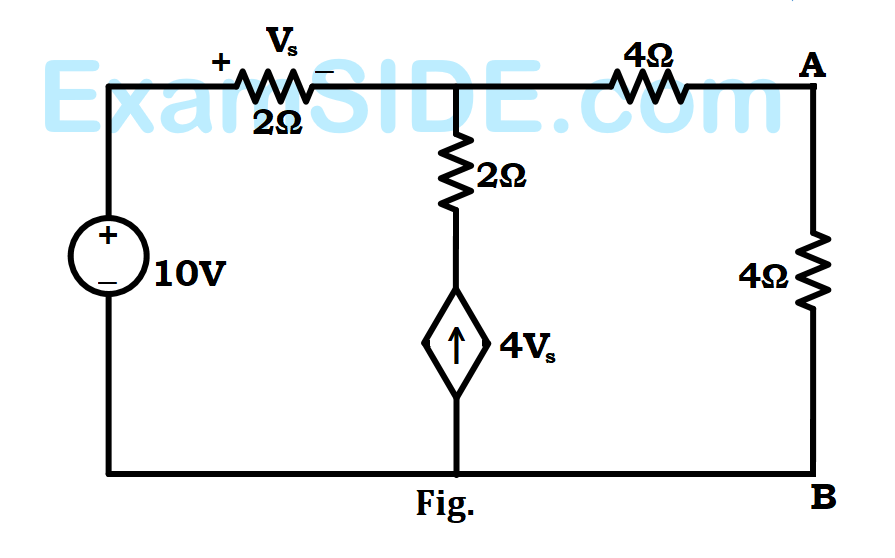
Find the Thevenin equivalent about $$AB$$ for the circuit shown in Figure.

Questions Asked from Network Theorems (Marks 5)
Number in Brackets after Paper Indicates No. of Questions
GATE EE Subjects
Electric Circuits
Electromagnetic Fields
Signals and Systems
Electrical Machines
Engineering Mathematics
General Aptitude
Power System Analysis
Electrical and Electronics Measurement
Analog Electronics
Control Systems
Power Electronics