GATE CSE 2007 | Finite Automata and Regular Language Question 62 | Theory of Computation

GATE CSE 2007

MCQ (Single Correct Answer)

-0.6

Consider the following finite state automation GATE CSE 2007 Theory of Computation - Finite Automata and Regular Language Question 61 English

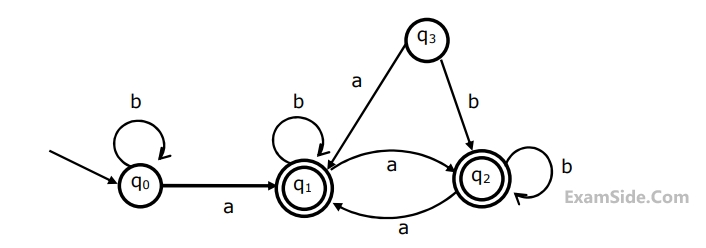
The language accepted by this automation is given by the regular expression

$${b^ * }a{b^ * }a{b^ * }a{b^ * }$$

$${\left( {a + b} \right)^ * }$$

$${b^ * }a{\left( {a + b} \right)^ * }$$

$${b^ * }a{b^ * }a{b^ * }$$

GATE CSE 2007

MCQ (Single Correct Answer)

-0.6

Consider the following finite state automation GATE CSE 2007 Theory of Computation - Finite Automata and Regular Language Question 60 English

The minimum state automation equivalent to the above $$FSA$$ has the following number of states

$$1$$

$$2$$

$$3$$

$$4$$

GATE CSE 2006

MCQ (Single Correct Answer)

-0.6

If $$s$$ is a string over $${\left( {0 + 1} \right)^ * }$$ then let $${n_0}\left( s \right)$$ denote the number of $$0'$$ s in $$s$$ and $${n_1}\left( s \right)$$ the number of $$1'$$s in $$s.$$ Which one of the following languages is not regular?

$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {{n_0}\left( s \right)\,\,} \right.} \right.$$ is a $$3$$-digit prime$$\left. \, \right\}$$

$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {\,\,} \right.} \right.$$ for every prefix $$s'$$ of $$s.$$ $$\,\left| {{n_0}\left( {{s^,}} \right) - {n_1}\left( {{s^,}} \right)\left| { \le \left. 2 \right\}} \right.} \right.$$

$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^*}\left\| {{n_0}\left( s \right) - {n_1}\left( s \right)\left| { \le \left. 4 \right\}} \right.} \right.} \right.$$

$$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }} \right.\left| {{n_0}\left( s \right)} \right.$$ mod $$7 = {n_1}\left( s \right)$$ mod $$5 = \left. 0 \right\}$$

GATE CSE 2006

MCQ (Single Correct Answer)

-0.6

Consider the regular language $$L = {\left( {111 + 11111} \right)^ * }.$$ The minimum number of states in any $$DFA$$ accepting this language is

$$3$$

$$5$$

$$8$$

$$9$$

PREVIOUS NEXT