A 10 kHz even-symmetric square wave is passed through a bandpass filter with centre frequency at 30 kHz and 3 dB passband of 6 kHz. The filter output is

Let f(t) be a continuous time signal and let F($$\omega$$) be its Fourier Transform defined by $$F\left(\omega\right)=\int_{-\infty}^\infty f\left(t\right)e^{-j\omega t}dt$$. Define g(t) by $$g\left(t\right)=\int_{-\infty}^\infty F\left(u\right)e^{-jut}du$$. What is the relationship between f(t) and g(t)?

The Fourier transform of a signal h(t) is $$H\left(j\omega\right)=\left(2\cos\omega\right)\left(\sin2\omega\right)/\omega$$. The value of h(0) is

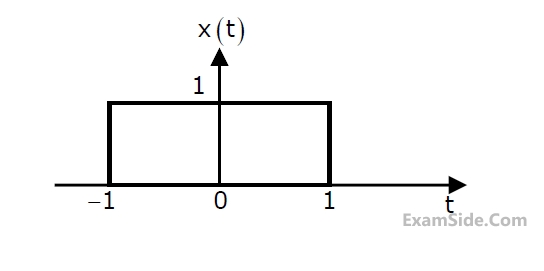
x(t) is a positive rectangular pulse from t = -1 to t = +1 with unit height as shown in the figure. The value of $$\int_{-\infty}^\infty\left|X\left(\omega\right)\right|^2d\omega$$ {where X($$\mathrm\omega$$) is the Fourier transform of x(t)} is