1
GATE EE 2003
MCQ (Single Correct Answer)
+1
-0.3
In the circuit of figure shown, assume that the transistor has $${h_{fe}} = 99$$ and $${V_{BE}} = 0.7V.$$
The value of collector current $${{\rm I}_C}$$ of the transistor is approximately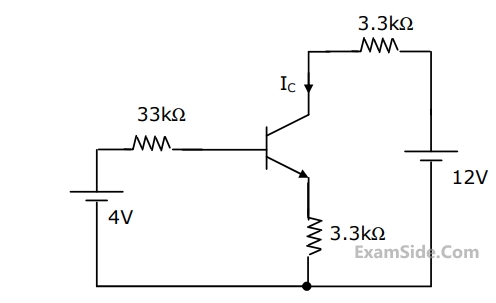
The value of collector current $${{\rm I}_C}$$ of the transistor is approximately

2
GATE EE 2003
MCQ (Single Correct Answer)
+2
-0.6
A voltage signal $$\,10\,\,\sin \,\omega t\,\,$$ is applied to the circuit with ideal diodes, as shown in figure. The maximum and minimum values of the output waveform of the circuit are respectively
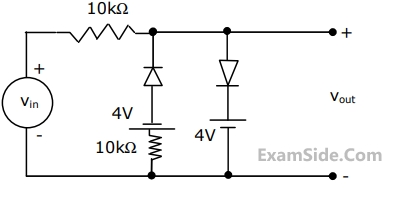

3
GATE EE 2003
MCQ (Single Correct Answer)
+1
-0.3
A lead compensator used for a closed loop controller has the following transfer function $${\textstyle{{K\left( {1 + {s \over a}} \right)} \over {\left( {1 + {s \over b}} \right)}}}\,\,\,$$ For such a lead compensator
4
GATE EE 2003
MCQ (Single Correct Answer)
+2
-0.6
The following equation defines a separately exited $$dc$$ motor in the form of a differential equation $${{{d^2}\omega } \over {d{t^2}}} + {{B\,d\omega } \over {j\,\,dt}} + {{{K^2}} \over {LJ}}\omega = {K \over {LJ}}{V_a}$$
The above equation may be organized in the state space form as follows
$$\left( {\matrix{
{{{{d^2}\omega } \over {d{t^2}}}} \cr
{{{d\omega } \over {dt}}} \cr
} } \right) = P\left( {\matrix{
{{{d\omega } \over {dt}}} \cr
\omega \cr
} } \right) + Q{V_a}$$
where the $$P$$ matrix is given by
Paper analysis
Total Questions
Analog Electronics
8
Control Systems
10
Digital Electronics
5
Electric Circuits
10
Electrical and Electronics Measurement
10
Electrical Machines
14
Electromagnetic Fields
4
Power Electronics
7
Power System Analysis
17
More papers of GATE EE
GATE EE 2025
GATE EE 2024
GATE EE 2023
GATE EE 2022
GATE EE 2021
GATE EE 2020
GATE EE 2019
GATE EE 2018
GATE EE 2017 Set 1
GATE EE 2017 Set 2
GATE EE 2016 Set 2
GATE EE 2016 Set 1
GATE EE 2015 Set 1
GATE EE 2015 Set 2
GATE EE 2014 Set 3
GATE EE 2014 Set 2
GATE EE 2014 Set 1
GATE EE 2013
GATE EE 2012
GATE EE 2011
GATE EE 2010
GATE EE 2009
GATE EE 2008
GATE EE 2007
GATE EE 2006
GATE EE 2005
GATE EE 2004
GATE EE 2003
GATE EE 2002
GATE EE 2001
GATE EE 2000
GATE EE 1999
GATE EE 1998
GATE EE 1997
GATE EE 1996
GATE EE 1995
GATE EE 1994
GATE EE 1993
GATE EE 1992
GATE EE 1991
GATE EE
Papers
2025
2024
2023
2022
2021
2020
2019
2018
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991