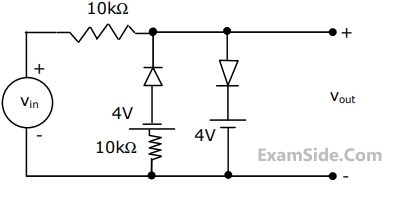
A voltage signal $$\,10\,\,\sin \,\omega t\,\,$$ is applied to the circuit with ideal diodes, as shown in figure. The maximum and minimum values of the output waveform of the circuit are respectively

A lead compensator used for a closed loop controller has the following transfer function $${\textstyle{{K\left( {1 + {s \over a}} \right)} \over {\left( {1 + {s \over b}} \right)}}}\,\,\,$$ For such a lead compensator

The following equation defines a separately exited $$dc$$ motor in the form of a differential equation $${{{d^2}\omega } \over {d{t^2}}} + {{B\,d\omega } \over {j\,\,dt}} + {{{K^2}} \over {LJ}}\omega = {K \over {LJ}}{V_a}$$

The above equation may be organized in the state space form as follows
$$\left( {\matrix{ {{{{d^2}\omega } \over {d{t^2}}}} \cr {{{d\omega } \over {dt}}} \cr } } \right) = P\left( {\matrix{ {{{d\omega } \over {dt}}} \cr \omega \cr } } \right) + Q{V_a}$$

where the $$P$$ matrix is given by

A second order system starts with an initial condition of $$\left( {\matrix{ 2 \cr 3 \cr } } \right)$$ without any external input. The state transition matrix for the system is given by $$\left( {\matrix{ {{e^{ - 2t}}} & 0 \cr 0 & {{e^{ - t}}} \cr } } \right).$$ The state of the system at the end of $$1$$ second is given by.