The ROC (region of convergence) of the z-transform of a discrete-time signal is represented by the shaded region in the z-plane. If the signal $$x\left[ n \right] = \,{\left( {2.0} \right)^{\left| n \right|}}$$ , $$ - \infty < n < + \infty $$ then the ROC of its z-transform is represented by

Consider the signal $$\,x\left( t \right)$$ $$\,\,\, = \,\,\,\cos \left( {6\pi t} \right)\,\, + \,\,\sin \left( {8\pi t} \right),$$ where $$\,t$$ is in seconds. The Nyquist sampling rate (in samples/second) for the signal $$y\left( t \right)\, = x\,\,\left( {2t + 5} \right)$$ is

The direct form structure of an FIR (finite impulse response) filter is shown in the figure.

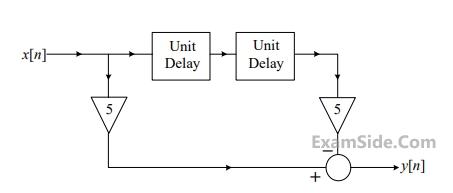
The filter can be used to approximate a

If the signal x(t) = $${{\sin (t)} \over {\pi t}}*{{\sin (t)} \over {\pi t}}$$ with * denoting the convolution operation, then x(t) is equal to