1
GATE CSE 2004
MCQ (Single Correct Answer)
+2
-0.6
What is the number of vertices in an undirected connected graph with $$27$$ edges, $$6$$ vertices of degree $$2$$, $$\,\,$$ $$3$$ vertices of degree 4 and remaining of degree 3?
2
GATE CSE 2004
MCQ (Single Correct Answer)
+2
-0.6
How many graphs on $$n$$ labeled vertices exist which have at least $$\left( {{n^2} - 3n} \right)/2\,\,\,$$ edges?
3
GATE CSE 2004
MCQ (Single Correct Answer)
+2
-0.6
The minimum number of colours required to colour the following graph, such that
no two adjacent vertices are assigned the same colour, is
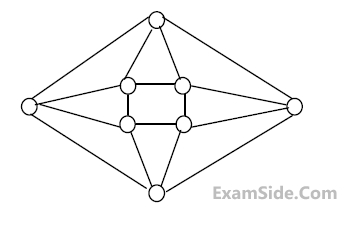

4
GATE CSE 2003
MCQ (Single Correct Answer)
+2
-0.6
$$A$$ graph $$G$$ $$=$$ $$(V, E)$$ satisfies $$\left| E \right| \le \,3\left| V \right| - 6.$$ The min-degree of $$G$$ is defined as $$\mathop {\min }\limits_{v \in V} \left\{ {{{\mathop{\rm d}\nolimits} ^ \circ }egree\left( v \right)} \right\}$$. Therefore, min-degree of $$G$$ cannot be
Questions Asked from Graph Theory (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE CSE 2024 Set 2 (1)
GATE CSE 2024 Set 1 (2)
GATE CSE 2023 (2)
GATE CSE 2022 (4)
GATE CSE 2021 Set 2 (1)
GATE CSE 2021 Set 1 (3)
GATE CSE 2020 (1)
GATE CSE 2019 (1)
GATE CSE 2015 Set 1 (2)
GATE CSE 2015 Set 2 (2)
GATE CSE 2014 Set 3 (2)
GATE CSE 2014 Set 1 (2)
GATE CSE 2014 Set 2 (1)
GATE CSE 2013 (1)
GATE CSE 2012 (2)
GATE CSE 2010 (1)
GATE CSE 2008 (5)
GATE CSE 2007 (2)
GATE CSE 2006 (3)
GATE CSE 2005 (1)
GATE CSE 2004 (4)
GATE CSE 2003 (2)
GATE CSE 2001 (1)
GATE CSE 1995 (1)
GATE CSE 1992 (1)
GATE CSE 1991 (1)
GATE CSE 1990 (1)
GATE CSE 1989 (1)
GATE CSE Subjects
Theory of Computation
Operating Systems
Algorithms
Database Management System
Data Structures
Computer Networks
Software Engineering
Compiler Design
Web Technologies
General Aptitude
Discrete Mathematics
Programming Languages