Suppose we run Dijkstra’s single source shortest-path algorithm on the following edge-weighted directed graph with vertex P as the source.
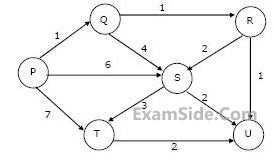In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?

Let G=(V,E) be an undirected graph with a subgraph G₁=(V₁,E₁). Weights are assigned to edges of G as follows. $$$w(e) = \begin{cases} 0 \text{, if } e \in E_1 \\1 \text{, otherwise} \end{cases}$$$ A single-source shortest path algorithm is executed on the weighted graph (V,E,w) with an arbitrary vertex v1 of V₁ as the source. Which of the following can always be inferred from the path costs computed?

Let G = (V, E) be a directed graph with n vertices. A path from v_i to v_j in G is sequence of vertices (v_i, v_i+1, ……., v_j) such that (v_k, v_k+1) ∈ E for all k in i through j – 1. A simple path is a path in which no vertex appears more than once. Let A be an n x n array initialized as follow
$$$A[j,k] = \left\{ {\matrix{ {1\,if\,(j,\,k)} \cr {1\,otherwise} \cr } } \right.$$$ Consider the following algorithm.

for i = 1 to n
   for j = 1 to n
      for k = 1 to n
         A [j , k] = max (A[j, k] (A[j, i] + A [i, k]); 

Which of the following statements is necessarily true for all j and k after terminal of the above algorithm ?

What is the weight of a minimum spanning tree of the following graph?