$$G = (V,E)$$ is an undirected simple graph in which each edge has a distinct weight, and e is a particular edge of G. Which of the following statements about the minimum spanning trees $$(MSTs)$$ of $$G$$ is/are TRUE?

$$\,\,\,\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,\,\,\,$$ If $$e$$ is the lightest edge of some cycle in $$G,$$ then every $$MST$$ of $$G$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$includes $$e$$
$$\,\,\,\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,\,\,\,$$ If $$e$$ is the heaviest edge of some cycle in $$G,$$ then every $$MST$$ of $$G$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$excludes $$e$$

Consider the weighted undirected graph with $$4$$ vertices, where the weight of edge $$\left\{ {i,j} \right\}$$ is given by the entry $${W_{ij}}$$ in the matrix $$W.$$ $$$W = \left[ {\matrix{ 0 & 2 & 8 & 5 \cr 2 & 0 & 5 & 8 \cr 8 & 5 & 0 & X \cr 5 & 8 & X & 0 \cr } } \right]$$$

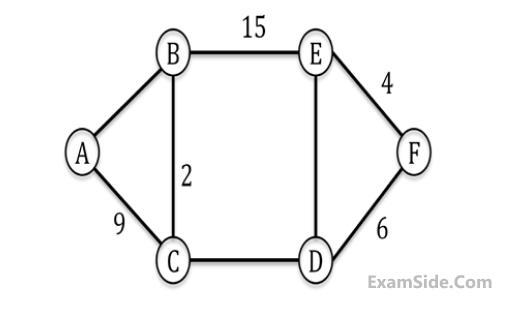
The largest possible integer value of $$x,$$ for which at least one shortest path between some pair of vertices will contain the edge with weight $$x$$ is _________________.

A Young tableau is a $$2D$$ array of integers increasing from left to right and from top to bottom. Any unfilled entries are marked with $$\infty ,$$ and hence there cannot be any entry to the right of, or below a $$\infty .$$ The following Young tableau consists of unique entries.

1	2	5	14
3	4	6	23
10	12	18	25
31	∞	∞	∞

When an element is removed from a Young tableau, other elements should be moved into its place so that the resulting table is still a Young tableau (unfilled entries may be filled in with a $$\infty $$). The minimum number of entries (other than $$1$$) to be shifted, to remove $$1$$ from the given Young tableau is ______________.

The graph shown below has 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ___________.