E = {(vi, vj) | 1 ≤ i < j ≤ 100}, and weight of the edge (vi, vj) is |i - j|. The weight of the minimum spanning tree of G is ______.
Consider the following undirected graph $$G: $$
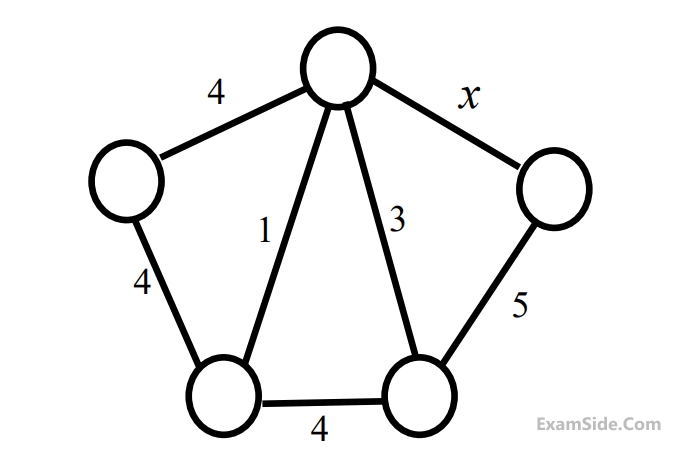
Choose a value for $$x$$ that will maximize the number of minimum weight spanning trees $$(MWSTs)$$ of $$G.$$ The number of $$MWSTs$$ of $$G$$ for this value of $$x$$ is ______.
| Item number | Weight (in Kgs) |
Value (in Rupees) |
|---|---|---|
| 1 | 10 | 60 |
| 2 | 7 | 28 |
| 3 | 4 | 20 |
| 4 | 2 | 24 |
The task is to pick a subset of these items such that their total weight is no more than $$11$$ $$Kgs$$ and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by $$V$$opt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by $$V$$greedy.
The value of $$V$$opt $$−$$ $$V$$greedy is ____________.