GATE CSE 2021 Set 2 | Complexity Analysis and Asymptotic Notations Question 8 | Algorithms

PREVIOUS NEXT

GATE CSE 2021 Set 2

MCQ (Single Correct Answer)

-0.66

For constants a ≥ 1 and b > 1, consider the following recurrence defined on the non-negative integers :

$$T\left( n \right) = a.T\left( {\frac{n}{b}} \right) + f\left( n \right)$$

Which one of the following options is correct about the recurrence T(n)?

If f(n) is $$\frac{n}{{{{\log }_2}(n)}}$$, then T(n) is θ(log₂(n)).

If f(n) is n log₂(n), then T(n) is θ(n log₂(n)).

If f(n) is O(n^{log_b(a) - ϵ}) for some ϵ > 0, then T(n) is θ(n^logb(a)).

If f(n) is θ(n^logb^(a)), then T(n) is θ(n^log^b^(a))

GATE CSE 2021 Set 1

MCQ (Single Correct Answer)

-0.67

Consider the following recurrence relation.

$$T(n) = \left\{ {\begin{array}{*{20}{c}} {T(n/2) + T(2n/5) + 7n \ \ \ if\ n > 0}\\ {1\ \ \ \ \ \ \ if\ n = 0} \end{array}} \right.$$

Which one of the following option is correct?

T(n) = Θ(n log n)

T(n) = Θ(n^5/2)

T(n) = Θ((log n)^5/2)

T(n) = Θ(n)

GATE CSE 2019

MCQ (Single Correct Answer)

-0.67

There are n unsorted arrays : A₁, A₂, …, A_n. Assume that n is odd. Each of A₁, A₂, …, A_n contains n distinct elements. There are no common elements between any two arrays. The worst-case time complexity of computing the median of the medians of A₁, A₂, …, A_n is :

$$O\left( n \right)$$

$$O\left( {n\log n} \right)$$

$$O\left( {{n^2}\log n} \right)$$

$$O\left( {{n^2}} \right)$$

GATE CSE 2016 Set 2

Numerical

-0

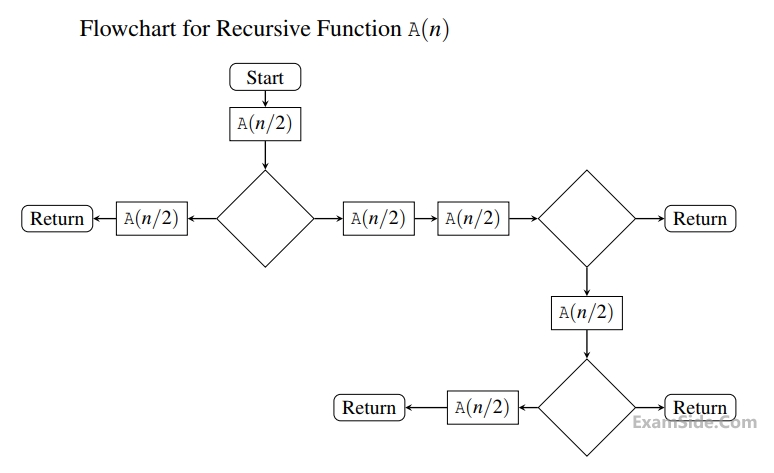
The given diagram shows the flowchart for a recursive function $$A(n).$$ Assume that all statements, except for the recursive calls, have $$O(1)$$ time complexity. If the worst case time complexity of this function is $$O\left( {{n^\alpha }} \right),$$ then the least possible value (accurate up to two decimal positions) of $$\alpha $$ is ____________ . GATE CSE 2016 Set 2 Algorithms - Complexity Analysis and Asymptotic Notations Question 13 English