GATE CSE 2021 Set 1 | Complexity Analysis and Asymptotic Notations Question 12 | Algorithms

GATE CSE 2021 Set 1

MCQ (Single Correct Answer)

-0.67

Consider the following recurrence relation.

$$T(n) = \left\{ {\begin{array}{*{20}{c}} {T(n/2) + T(2n/5) + 7n \ \ \ if\ n > 0}\\ {1\ \ \ \ \ \ \ if\ n = 0} \end{array}} \right.$$

Which one of the following option is correct?

T(n) = Θ(n log n)

T(n) = Θ(n^5/2)

T(n) = Θ((log n)^5/2)

T(n) = Θ(n)

GATE CSE 2019

MCQ (Single Correct Answer)

-0.67

There are n unsorted arrays : A₁, A₂, …, A_n. Assume that n is odd. Each of A₁, A₂, …, A_n contains n distinct elements. There are no common elements between any two arrays. The worst-case time complexity of computing the median of the medians of A₁, A₂, …, A_n is :

$$O\left( n \right)$$

$$O\left( {n\log n} \right)$$

$$O\left( {{n^2}\log n} \right)$$

$$O\left( {{n^2}} \right)$$

GATE CSE 2016 Set 2

Numerical

-0

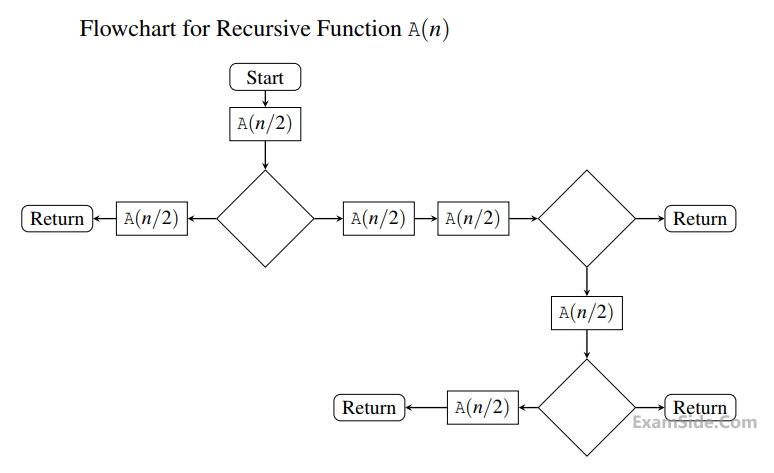
The given diagram shows the flowchart for a recursive function $$A(n).$$ Assume that all statements, except for the recursive calls, have $$O(1)$$ time complexity. If the worst case time complexity of this function is $$O\left( {{n^\alpha }} \right),$$ then the least possible value (accurate up to two decimal positions) of $$\alpha $$ is ____________ . GATE CSE 2016 Set 2 Algorithms - Complexity Analysis and Asymptotic Notations Question 16 English

GATE CSE 2016 Set 2 Algorithms - Complexity Analysis and Asymptotic Notations Question 16 English

Your input ____

GATE CSE 2015 Set 3

MCQ (Single Correct Answer)

-0.6

Let $$f\left( n \right) = n$$ and $$g\left( n \right) = {n^{\left( {1 + \sin \,\,n} \right)}},$$ where $$n$$ is a positive integer. Which of the following statements is/are correct?

$$\eqalign{ & \,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,f\left( n \right) = O\left( {g\left( n \right)} \right) \cr & \,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,f\left( n \right) = \Omega \left( {g\left( n \right)} \right) \cr} $$

Only $${\rm I}$$

Only $${\rm I}$$$${\rm I}$$

both $${\rm I}$$ and $${\rm I}$$$${\rm I}$$

Neither $${\rm I}$$ nor $${\rm I}$$$${\rm I}$$

PREVIOUS NEXT