For the transfer function G$$\left( {j\omega } \right) = 5 + j\omega ,$$ the corresponding Nyquist plot for positive frequency has the form

The input-output transfer function of a plant is h(s)=$${{100} \over {s{{\left( {s + 10} \right)}^2}}}$$. The plant is placed in a unity negative feedback configuration as shown in the figure below. The gain margin of the system under closed loop unity negative feedback is

The input-output transfer function of a plant is h(s)=$${{100} \over {s{{\left( {s + 10} \right)}^2}}}$$. The plant is placed in a unity negative feedback configuration as shown in the figure below. The signal flow graph that DOES NOT model the plant transfer function H(s) is

The block diagram of a system with one input u and two outputs y₁ and y₂ is given below

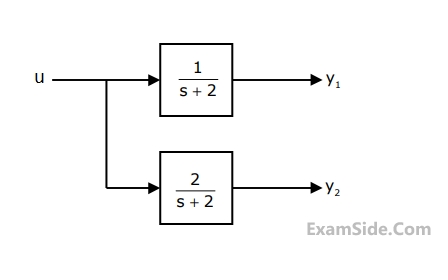
A state space model of the above system in terms of the state vector $$\underline x $$ and the output vector $$\underline y = {\left[ {\matrix{ {{y_1}} & {{y_2}} \cr } } \right]^\tau }$$ is