The relation scheme student Performance (Name, CourseNo, RollNo, Grade) has the following functional dependencies:

Name, courseNo $$\,\, \to \,\,$$ grade
RollNo, courseNo $$\,\, \to \,\,$$ grade
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,\,\,\,\,\,$$ Name $$\,\, \to \,\,$$ rollNo
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,\,\,\,\,\,$$ RollNo $$\,\, \to \,\,$$ name

The highest normal form of this relation scheme is

A relation Empdt $$1$$ is defined with attributes empcode (unique), name, street, city, state and pincode. For any pincode, there is only one city and state. Also, for any given street city and the state, there is just one pincode. In normalization terms, Empdt$$1$$ is a relation in

Consider the following functional dependencies in a database.
$$\eqalign{ & \,\,\,\,Date\,\,of\,\,Birth\,\, \to \,\,Age \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Age\,\, \to \,\,Eligibility \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Name\,\, \to \,\,Roll\_number \cr & \,\,\,\,\,Roll\_number\,\, \to \,\,Name \cr & Course\_number\, \to \,\,Course\_name \cr & Course\_number\, \to Instructor \cr & (Roll\_Number,\,Course\_number)\,\, \to \,\,Grade \cr} $$

The relation (Roll_number, Name, Date_of_Birth, Age) is

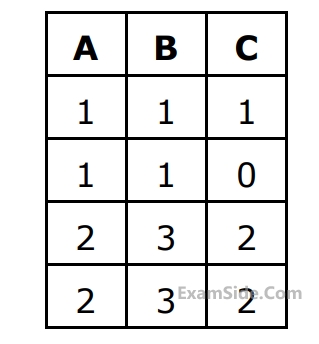
From the following instance of a relation schema $$R(A, B, C),$$ we can conclude that: