GATE CSE 2002 | Functional Dependencies and Normalization Question 38 | Database Management System

GATE CSE 2002

MCQ (Single Correct Answer)

-0.6

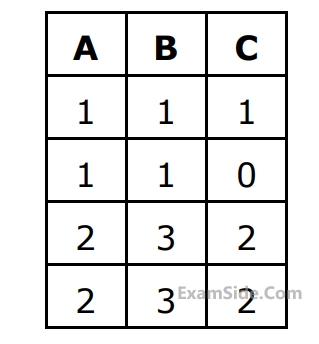
From the following instance of a relation schema $$R(A, B, C),$$ we can conclude that: GATE CSE 2002 Database Management System - Functional Dependencies and Normalization Question 30 English

GATE CSE 2002 Database Management System - Functional Dependencies and Normalization Question 30 English

A functionally determines $$B$$ and $$B$$ functionally determines $$C$$

A functionally determines $$B$$ and $$B$$ does not functionally determines $$C$$

$$B$$ does not functionally determines $$C$$

A does not functionally determine $$B$$ and $$B$$ does not functionally determine $$C$$

GATE CSE 2001

MCQ (Single Correct Answer)

-0.6

$$R(A,B,C,D)$$ is a relation. Which of the following does not have a lossless-join, dependency preserving $$BCNF$$ decomposition?

$$A \to B,\,B \to CD$$

$$A \to B,\,B \to C.\,C \to D$$

$$AB \to C,\,C \to AD$$

$$A \to BCD$$

GATE CSE 2000

MCQ (Single Correct Answer)

-0.6

Given the following relation instance
$$\eqalign{ & X\,\,\,\,\,Y\,\,\,\,\,Z \cr & \,\,1\,\,\,\,\,\,4\,\,\,\,\,\,2 \cr & \,\,1\,\,\,\,\,\,5\,\,\,\,\,\,3 \cr & \,\,1\,\,\,\,\,\,6\,\,\,\,\,\,3 \cr & \,\,3\,\,\,\,\,\,2\,\,\,\,\,\,2 \cr} $$

Which of the following functional dependencies are satisfied by the instance?

$$XY \to Z$$ and $$Z \to Y$$

$$YZ \to X$$ and $$Y \to Z$$

$$YZ \to X$$ and $$X \to Z$$

$$XZ \to Y$$ and $$Y \to X$$

GATE CSE 1999

MCQ (Single Correct Answer)

-0.6

Consider the schema $$R = \left( {S\,\,T\,\,U\,\,V} \right)$$ and the dependencies $$S \to T,\,\,T \to U,\,\,U \to V$$ and $$V \to S$$ let $$R =$$ $$(R1$$ and $$R2)$$ be a decomposition such that $$R1 \cap R2 \ne \phi .$$ The decomposition is:

Not in $$2NF$$

In $$2NF$$ but not $$3NF$$

In $$3NF$$ but not in $$2NF$$

In both $$2NF$$ and $$3NF$$

PREVIOUS NEXT