The procedure given below is required to find and replace certain characters inside an input character string supplied in array $$A.$$ The characters to be replaced are supplied in array $$oldc,$$ while their respective replacement characters are supplied in array $$newc.$$ Array $$A$$ has a fixed length of five characters, while arrays $$oldc$$ and $$newc$$ contain three characters each. However, the procedure is flawed. void find_and_replace (char $$^ * A,$$ char $$^ * oldc,$$, char $$^ * newc$$)
$$\left\{ \, \right.$$ for (int $$i=0; i<5; i++$$)
for (int $$j=0; j<3; j++$$)
if ( $$A$$ [ $$i$$ ] $$==oldc$$ [ $$j$$ ] $$A$$ [ $$i$$ ]
$$=newc$$ [ $$j$$ ]; $$\left. \, \right\}$$

The procedure is tested with the following four test cases;
$$\eqalign{ & \left( 1 \right)\,\,\,oldc = ''abc'',\,\,newc\, = \,''dab'' \cr & \left( 2 \right)\,\,\,oldc\, = \,''cdc'',\,\,newc\, = \,''bed'' \cr & \left( 3 \right)\,\,\,oldc\, = \,''bca'',\,newc\, = \,''cda'' \cr & \left( 4 \right)\,\,\,oldc\, = \,''abc'',\,newc\, = \,''bac'' \cr} $$

If array $$A$$ is made to hold the string $$''abcde'',$$ which of the above four test cases will be successful is exposing the flaw in this procedure?

The following is comment written for $$a$$ $$c$$ function. This function computes the roots of quadratic equation. $$a{x^2} + bx + c = 0$$ the function stores two real roots in $${}^ * root1\,\,\& \,\,{}^ * root2\,\,\,\& $$ returns the status of validity of roots. In handles four different kinds of cases
$$i)$$ When coefficient $$a$$ is zero or irrespective of discriminate
$$ii)$$ When discriminate is positive.
$$iii)$$ When discriminate is zero
$$iv)$$ When discriminate is negative

Only in cases $$(ii)$$ & $$(iii)$$ the stored roots are valid Otherwise $$0$$ is stored in the roots the function returns $$0$$ when the roots are valid & - $$1$$ otherwise. The function also ensures root $$1$$ $$> =$$ root $$2.$$

int get QuadRoots(float a, float b, float c, float $${}^ * root1$$, float $${}^ * root2$$);

A software test engineer is assigned the job of doing block box testing. He comes up with the following test cases, many of which are redundant

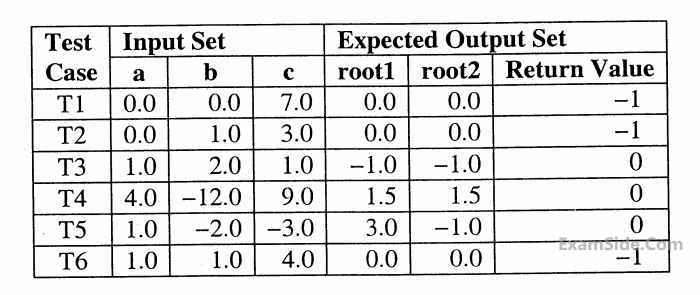
Which one of the following options provide the set of non-redundant tests using equivalence class partitioning approach from input perspective for black box testing?

The following program is to be tested for statement coverage:
begin
if $$\left( {a = \,\, = b} \right)\,\,\left\{ {S1;\,\,exit;} \right\}$$
else if $$\left( {c = \,\, = d} \right)\,\,\left\{ {S2;} \right\}$$
else $$\left\{ {S3;\,\,exit;} \right\}$$
$$S4;$$
end

The test cases $${T_1},\,{T_2},\,{T_3}\,\,\& \,{T_4}$$ given below are expressed in terms of the properties satisfied by the values of variables $$a, b, c$$ and $$d.$$ The exact values are not given.
$${T_1}:\,a,\,b,\,c\,\& \,d$$ are all equal
$${T_2}:\,a,\,b,\,c\,\& \,d$$ are all distinct
$${T_3}:\,a = b\,\,\,\& \,\,\,\,c\,!\, = \,d$$
$${T_4}:\,a! = b\,\,\,\& \,\,\,\,c\, = \,d$$

Which of the test suites given below ensures coverage of statements $${S_1},\,{S_2},\,{S_3}\,\,\& \,{S_4}$$ ?

Consider the following statements about the cyclomatic complexity of the control flow graph of a program module. Which of these are TRUE?

$${\rm I}.\,\,\,\,\,\,$$ The cyclomatic complexity of a module is equal to the maximum number of
$$\,\,\,\,\,\,\,\,\,\,\,$$linearly independent circuits in the graph.
$${\rm II}.\,\,\,$$ The cyclomatic complexity of a module is the number of decisions in the
$$\,\,\,\,\,\,\,\,\,\,$$module plus one, where a decision is effectively any conditional statement in
$$\,\,\,\,\,\,\,\,\,\,$$the module.
$${\rm III}\,$$ The cyclomatic complexity can also be used as a number of linearly
$$\,\,\,\,\,\,\,\,\,\,$$independent paths that should be tested during path coverage testing.