A curve passes through the point ($$x$$ = 1, $$y$$ = 0) and satisfies the differential equation

$${{dy} \over {dx}} = {{{x^2} + {y^2}} \over {2y}} + {y \over x}$$. The equation that describes the curve is

The contour C given below is on the complex plane $$z = x + jy$$, where $$j = \sqrt { - 1} $$. 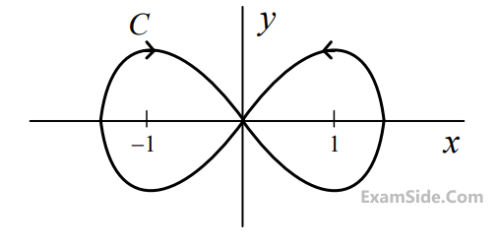The value of the integral $${1 \over {\pi j}}\oint\limits_C {{{dz} \over {{z^2} - 1}}} $$ is ________________.

Let X₁ , X₂ , X₃ and X₄ be independent normal random variables with zero mean and unit variance. The probability that X₄ is the smallest among the four is _______.

Taylor series expansion of $$f\left( x \right) = \int\limits_0^x {{e^{ - \left( {{{{t^2}} \over 2}} \right)}}} dt$$ around 𝑥 = 0 has the form

f(x) = $${a_0} + {a_1}x + {a_2}{x^2} + ...$$

The coefficient $${a_2}$$ (correct to two decimal places) is equal to _______.