1
GATE ECE 1996
Subjective
+5
-0
Refer to the circuit shown in Fig.
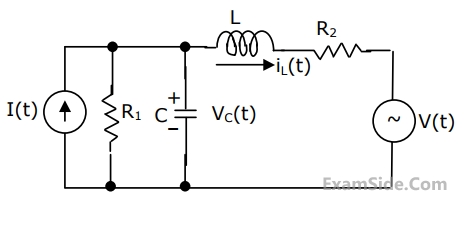 Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
 Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].
Choosing the voltage vC(t) across capacitor, and the current iL(t) through the inductor as state variable,i.e.,
$$$\left[\mathrm x\left(\mathrm t\right)\right]\;=\;\begin{bmatrix}{\mathrm v}_\mathrm C\left(\mathrm t\right)\\{\mathrm i}_\mathrm L\left(\mathrm t\right)\end{bmatrix}$$$
Write the state equation in the form $$\frac{\operatorname d\left[x\left(t\right)\right]}{\operatorname dt}\;=\;\left[A\right]\left[x\left(t\right)\right]\;+\;\left[B\right]\left[u\left(t\right)\right]$$ and find [A], [B] and [u(t)].2
GATE ECE 1996
Subjective
+3
-0
In the circuit shown in Fig (a) - (c), assuming initial voltages across capacitors and current through the inductors to be zero at the time of switching (t=0), then at any time t>0.

Match each of the items of Set 1, with the appropriate item of the Set 2.

Set 2
(1) current increases monotonically with time
(2) current decreases monotonically with time
(3) current remains constant at V/R
(4) current first increases, then decreases
(5) no current can ever flow
3
GATE ECE 1996
Subjective
+5
-0
In the circuit shown in Fig., it is known that the variable current source I absorbs power.Find I (in magnitude and direction) so that it receives maximum power and also find the amount of power absorbed by it.
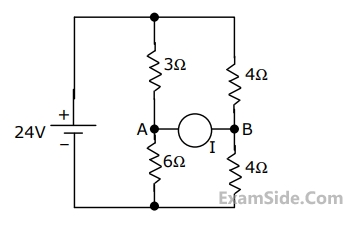
4
GATE ECE 1996
MCQ (Single Correct Answer)
+2
-0.6
The inverse Laplace transform of the function $${{s + 5} \over {\left( {s + 1} \right)\left( {s + 3} \right)}}$$ is
Paper analysis
Total Questions
Analog Circuits
8
Communications
1
Control Systems
2
Digital Circuits
6
Electromagnetics
10
Engineering Mathematics
1
Microprocessors
2
Network Theory
9
Signals and Systems
9
More papers of GATE ECE
GATE ECE 2025
GATE ECE 2024
GATE ECE 2023
GATE ECE 2022
GATE ECE 2021
GATE ECE 2019
GATE ECE 2018
GATE ECE 2017 Set 2
GATE ECE 2017 Set 1
GATE ECE 2016 Set 3
GATE ECE 2016 Set 2
GATE ECE 2016 Set 1
GATE ECE 2015 Set 2
GATE ECE 2015 Set 3
GATE ECE 2015 Set 1
GATE ECE 2014 Set 1
GATE ECE 2014 Set 4
GATE ECE 2014 Set 3
GATE ECE 2014 Set 2
GATE ECE 2013
GATE ECE 2012
GATE ECE 2011
GATE ECE 2010
GATE ECE 2009
GATE ECE 2008
GATE ECE 2007
GATE ECE 2006
GATE ECE 2005
GATE ECE 2004
GATE ECE 2003
GATE ECE 2002
GATE ECE 2001
GATE ECE 2000
GATE ECE 1999
GATE ECE 1998
GATE ECE 1997
GATE ECE 1996
GATE ECE 1995
GATE ECE 1994
GATE ECE 1993
GATE ECE 1992
GATE ECE 1991
GATE ECE 1990
GATE ECE 1989
GATE ECE 1988
GATE ECE 1987
GATE ECE
Papers
2025
2024
2023
2022
2021
2019
2018
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987