Which one of the following hash functions on integers will distribute keys most uniformly over $$10$$ buckets numbered $$0$$ to $$9$$ for $$𝑖$$ ranging from $$0$$ to $$2020$$?

Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?

Consider a hash table with 9 slots. The hash function is h(k) = k mod 9. The collisions are resolved by chaining. The following 9 keys are inserted in the order: 5, 28, 19, 15, 20, 33, 12, 17, 10. The maximum, minimum, and average chain lengths in the hash table, respectively, are

A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below 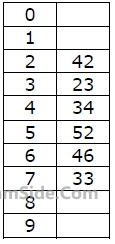How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?