Consider the following undirected graph with edge weights as shown:

The number of minimum-weight spanning trees of the graph is ______

Breadth First Search $$(BFS)$$ is started on a binary tree beginning from the root vertex. There is a vertex $$t$$ at a distance four from the root. If t is the $$n$$-th vertex in this $$BFS$$ traversal, then the maximum possible value of $$n$$ is ___________.

Consider the following directed graph:

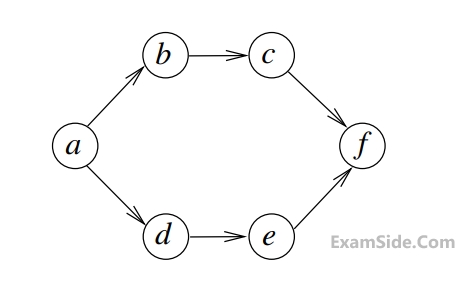
The number of different topological orderings of the vertices of the graph is ________________.

Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.