Consider a network with five nodes, N1 to N5, as shown below.

The network uses a Distance Vector Routing protocol. Once the routes have stabilized, the distance vectors at different nodes are as following

N1 : ( 0, 1, 7, 8, 4 )
N2 : ( 1, 0, 6, 7, 3 )
N3 : ( 7, 6, 0, 2, 6 )
N4 : ( 8, 7, 2, 0, 4 )
N5 : ( 4, 3, 6, 4, 0 )

Each distance vector is the distance of the best known path at that instance to nodes, N1 to N5, where the distance to itself is 0. Also, all links are symmetric and the cost is identical in both directions. In each round, all nodes exchange their distance vectors with their respective neighbors. Then all nodes update their distance vectors. In between two rounds, any change in cost of a link will cause the two incident nodes to change only that entry in their distance vectors

After the update in the previous question, the link N1-N2 goes down. N2 will reflect this change immediately in its distance vector as cost, $$\infty $$. After the NEXT ROUND of update, what will be the cost to N1 in the distance vector of N3?

Consider a network with five nodes, N1 to N5, as shown below.

The network uses a Distance Vector Routing protocol. Once the routes have stabilized, the distance vectors at different nodes are as following

N1 : ( 0, 1, 7, 8, 4 )
N2 : ( 1, 0, 6, 7, 3 )
N3 : ( 7, 6, 0, 2, 6 )
N4 : ( 8, 7, 2, 0, 4 )
N5 : ( 4, 3, 6, 4, 0 )

Each distance vector is the distance of the best known path at that instance to nodes, N1 to N5, where the distance to itself is 0. Also, all links are symmetric and the cost is identical in both directions. In each round, all nodes exchange their distance vectors with their respective neighbors. Then all nodes update their distance vectors. In between two rounds, any change in cost of a link will cause the two incident nodes to change only that entry in their distance vectors

The cost of link N2 - N3 reduces to 2 in (both directions). After the next round of updates, what will be the new distance vector at node, N3?

Consider a network with 6 routers R1 to R6 connected with links having weights as shown in the following diagram

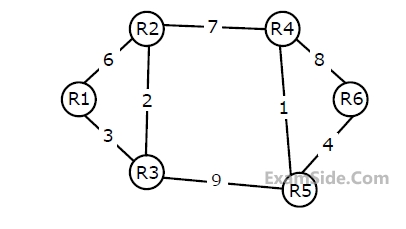
All the routers use the distance vector based routing algorithm to update their routing tables. Each router starts with its routing table initialized to contain an entry for each neighbour with the weight of the respective connecting link. After all the routing tables stabilize, how many links in the network will never be used for carrying any data?

Consider a network with 6 routers R1 to R6 connected with links having weights as shown in the following diagram

Suppose the weights of all unused links in the previous question are changed to 2 and the distance vector algorithm is used again until all routing tables stabilize. How many links will now remain unused?