1
GATE CSE 2021 Set 1
MCQ (Single Correct Answer)
+2
-0.67
| Items | Cost | Profit% | Marked price |
|---|---|---|---|
| P | 5400 | - | 5860 |
| Q | - | 25 | 10000 |
Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3 : 4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost
(Profit% = $${{Selling\,price - Cost} \over {Cost}} \times 100$$).
The discount on item Q, as a percentage of its marked price, is ________.
2
GATE CSE 2020
MCQ (Single Correct Answer)
+2
-0.67
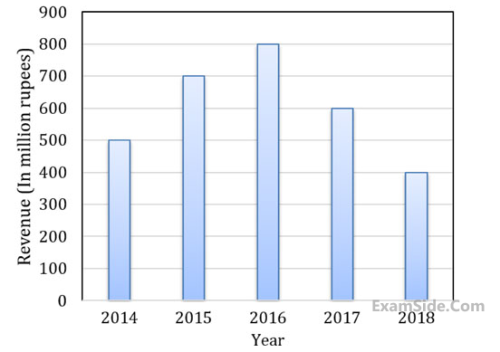
The total revenue of a company during 2014-2018 is shown in the bar graph. If the total expenditure of the company in each year is 500 million rupees, then the aggregate profit or loss (in percentage) on the total expenditure of the company during 2014-2018 is ______.

3
GATE CSE 2020
MCQ (Single Correct Answer)
+2
-0.67
Two straight lines are drawn perpendicular to each other in X-Y plane. If $$\alpha $$ and $$\beta $$ are the acute angles the straight lines make with the X-axis, then $$\alpha $$ + $$\beta $$ is ______.
4
GATE CSE 2020
MCQ (Single Correct Answer)
+2
-0.67
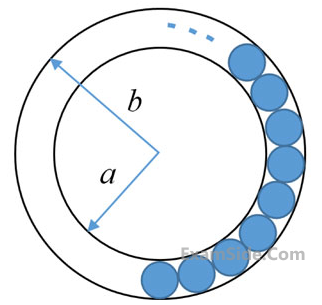
The figure below shows an annular ring with outer and inner radii as b and a, respectively. The annular space has been painted in the form of blue colour circles touching the outer and inner periphery of annular space. If maximum n number of circles can be painted, then the unpainted area available in annular space is _______.

Questions Asked from Numerical Ability (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE CSE 2025 Set 2 (2)
GATE CSE 2025 Set 1 (3)
GATE CSE 2024 Set 2 (2)
GATE CSE 2024 Set 1 (4)
GATE CSE 2023 (2)
GATE CSE 2022 (1)
GATE CSE 2021 Set 2 (2)
GATE CSE 2021 Set 1 (3)
GATE CSE 2020 (3)
GATE CSE 2019 (1)
GATE CSE 2018 (4)
GATE CSE 2017 Set 1 (3)
GATE CSE 2016 Set 1 (3)
GATE CSE 2015 Set 1 (3)
GATE CSE Subjects
Theory of Computation
Operating Systems
Algorithms
Database Management System
Data Structures
Computer Networks
Software Engineering
Compiler Design
Web Technologies
General Aptitude
Discrete Mathematics
Programming Languages