A three phase thyristor bridge rectifier is used in a $$HVDC$$ link. The firing angle $$\alpha $$ (as measured from the point of natural commutation) is constrained to lie between $${5^ \circ }$$ and $${30^ \circ }$$. If the $$dc$$ side current and $$ac$$ side voltage magnitude are constant, which of the following statements is true (neglect harmonics in the $$ac$$ side current and commutation overlap in your analysis)

A six pulse thyristor rectifier bridge is connected to a balanced $$50Hz$$ three phase $$ac$$ source. Assuming that the $$dc$$ output current of the rectifier is constant, the lowest frequency harmonic component in the $$ac$$ source line current is

A long wire composed of a smooth round conductor runs above and parallel to the ground (assumed to be a large conducting plane). A high voltage exists between the conductor and the ground. The maximum electric stress occurs at

Two transposed $$3$$ phase lines run parallel to each other. The equation describing the voltage drop in both lines is given below.

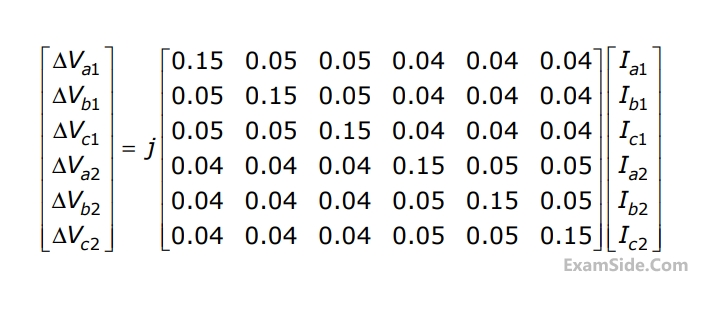
Compute the self and mutual zero sequence impedances of this system i.e, compute $${Z_{011}},\,\,{Z_{012}},\,\,{Z_{021}},\,\,{Z_{022}}\,\,\,$$ in the following equations.
$$\Delta {V_{01}} = {Z_{011}}\,{{\rm I}_{01}} + {Z_{012}}\,{{\rm I}_{02}}$$
$$\Delta {V_{02}} = {Z_{021}}\,{{\rm I}_{01}} + {Z_{022}}\,{{\rm I}_{02}}\,\,$$ where $$\,\Delta {V_{01}},$$
$$\Delta {V_{02}},\,{{\rm I}_{01}},\,{{\rm I}_{02}}\,\,$$ are the zero sequence voltage drops and currents for the two lines respectively.