The equivalent circuits of a diode, during forward and reverse biased conditions are shown in figure.
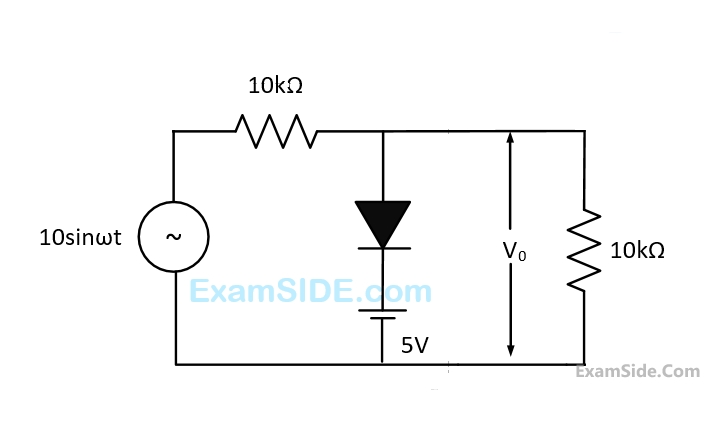
(a)
(b)

If such diodes are used in the clipper circuit of figure given above, the output voltage (V₀) of the circuit will be

The transfer function of a system is given as $${{100} \over {{s^2} + 20s + 100}}.$$ The system is

The state space equation of a system is described by $$\mathop X\limits^ \bullet = AX + BU,\,\,Y = Cx$$ where $$X$$ is state vector, $$U$$ is input, $$Y$$ is output and $$$A = \left( {\matrix{ 0 & 1 \cr 0 & { - 2} \cr } } \right)\,\,B = \left( {\matrix{ 0 \cr 1 \cr } } \right)\,\,C = \left[ {\matrix{ 1 & 0 \cr } } \right]$$$

A unity feedback is provided to the above system $$G(s)$$ to make it a closed loop system as shown in figure.

For a unit step input $$r(t),$$ the steady state error in the input will be

The state space equation of a system is described by $$\mathop X\limits^ \bullet = AX + BU,\,\,Y = Cx$$ where $$X$$ is state vector, $$U$$ is input, $$Y$$ is output and $$$A = \left( {\matrix{ 0 & 1 \cr 0 & { - 2} \cr } } \right)\,\,B = \left( {\matrix{ 0 \cr 1 \cr } } \right)\,\,C = \left[ {\matrix{ 1 & 0 \cr } } \right]$$$

The transfer function $$G(s)$$ of this system will be