The table below gives values of a function $$f(x)$$ obtained for values of $$x$$ at intervals of $$0.25$$

The value of the integral of the function between the limits $$0$$ to $$1,$$ using Simpson's rule is

The area under the curve shown between $$x=1$$ and $$x=5$$ is to be evaluated using the trapezoidal rule. The following points on the curve are given

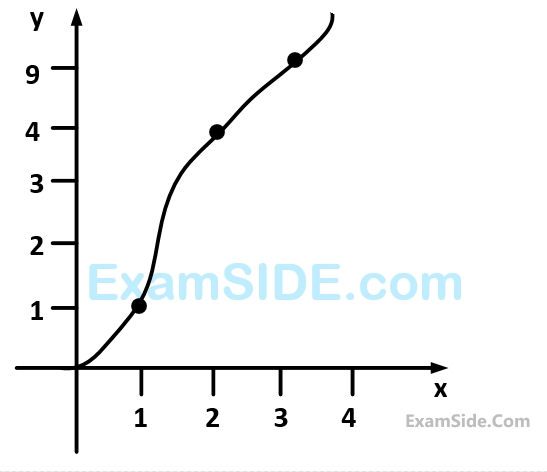
The evaluated area (In m²) will be

If the interval of integration is divided into two equal intervals of width $$1.0,$$ the value of the definite integral $$\,\,\int\limits_1^3 {\log _e^x\,\,dx\,\,\,\,} $$ using simpson's one $$-$$ third rule will be

Given $$a>0,$$ we wish to calculate its reciprocal value $${1 \over a}$$ by using Newton - Raphson method for $$f(x)=0.$$ For $$a=7$$ and starting with $${x_0} = 0.2\,\,$$ the first two iterations will be