Numerical Methods · Engineering Mathematics · GATE CE
Marks 1
The second derivative of a function $f$ is computed using the fourth-order Central Divided Difference method with a step length $h$. The CORRECT expression for the second derivative is
Consider the data of $f(x)$ given in the table.
| $i$ | $0$ | $1$ | $2$ |
|---|---|---|---|
| $x_i$ | $1$ | $2$ | $3$ |
| $f(x_i)$ | $0$ | $0.3010$ | $0.4771$ |
The value of $f(1.5)$ estimated using second-order Newton’s interpolation formula is ________________ (rounded off to 2 decimal places).
Consider the following recursive iteration scheme for different values of variable P with the initial guess x1 = 1:
$${x_{n + 1}} = {1 \over 2}\left( {{x_n} + {P \over {{x_n}}}} \right)$$, n = 1, 2, 3, 4, 5
For P = 2, x5 is obtained to be 1.414, rounded-off to three decimal places. For P = 3, x5 is obtained to be 1.732, rounded-off to three decimal places. If P = 10, the numerical value of x5 is __________. (round off to three decimal places)
Marks 2
Consider the differential equation given below. Using the Euler method with the step size (h) of 0.5 , the value of $y$ at $x=1.0$ is equal to _________ (rounded off to 1 decimal place).
$$ \frac{d y}{d x}=y+2 x-x^2 ; y(0)=1 \quad(0 \leq x<\infty) $$
A function f(x), that is smooth and convex-shaped between interval (xl , su) is shown in the figure. This function is observed at odd number of regularly spaced points. If the area under the function is computed numerically, then .
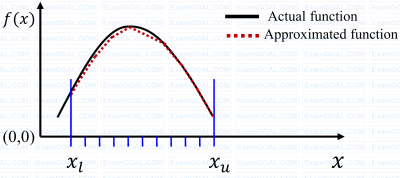
$$2x=3$$
$$4x=1$$

The value of the integral of the function between the limits $$0$$ to $$1,$$ using Simpson's rule is

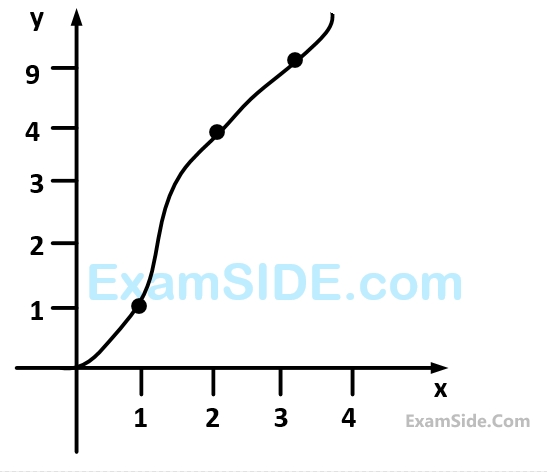
The evaluated area (In m2) will be