For $$\,\,\,{{{d^2}y} \over {d{x^2}}} + 4{{dy} \over {dx}} + 3y = 3{e^{2x}},\,\,$$ the particular integral is

Multiplication of matrices $$E$$ and $$F$$ is $$G.$$ Matrices $$E$$ and $$G$$ are
$$E = \left[ {\matrix{ {\cos \theta } & { - sin\theta } & 0 \cr {sin\theta } & {\cos \theta } & 0 \cr 0 & 0 & 1 \cr } } \right]$$ and $$G = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr } } \right]$$
What is the matrix $$F?$$

Eigen values of a matrix $$S = \left[ {\matrix{ 3 & 2 \cr 2 & 3 \cr } } \right]$$ are $$5$$ and $$1.$$ What are the eigen values of the matrix $${S^2} = SS?$$

The solution of the differential equation $${{dy} \over {dx}} + 2xy = {e^{ - {x^2}}}\,\,$$ with $$y(0)=1$$ is

If point A is in equilibrium under the action of the applied forces, the values of tensions and T _AB and T_AC are respectively.

A smooth flat plate with a sharp leading edge is placed along a gas stream flowing at $$U = 10\,m/s.$$ The thickness of the boundary layer at section $$r$$- $$s$$ is $$10$$ $$mm,$$ the breadth of the plate is $$1$$ $$m$$ (into the paper) and the density of the gas, $$\rho = 1.0\,kg/{m^3}.$$ Assume that the boundary layer is thin, two-dimensional, and follows a linear velocity distribution, $$u = U\left( {y/\delta } \right),$$ at the section $$r$$-$$s$$, where $$y$$ is the height from plate.

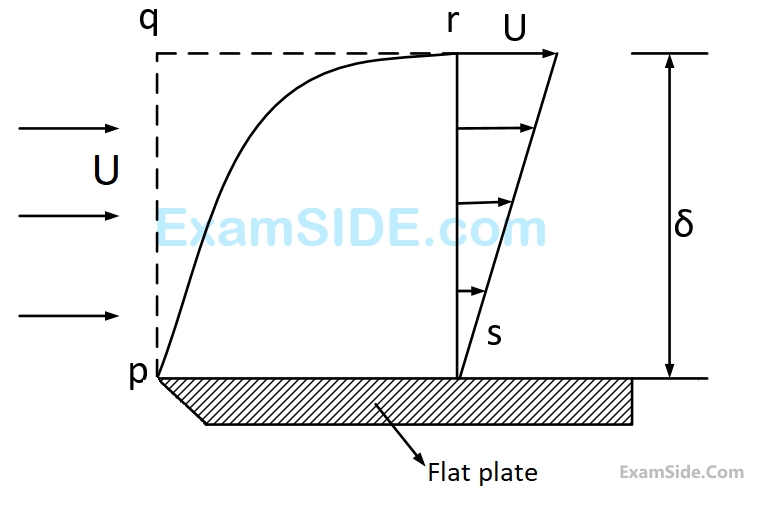
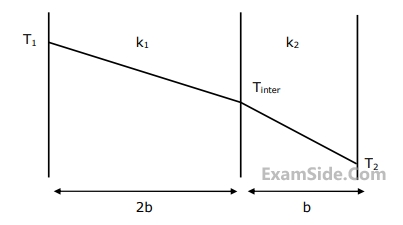
The integrated drag force (in $$N$$) on the plate, between $$p$$-$$s$$, is

For a Newtonian fluid:

A two-dimensional flow field has velocities along the $$x$$ and $$y$$ directions given by $$u = {x^2}t$$ and $$v = - 2xyt$$ respectively, where $$t$$ is time. The equation of streamline is

In a two-dimensional velocity field with velocities $$u$$ and $$v$$ along $$x$$ and $$y$$ directions respectively, the convective acceleration along the $$x$$-direction is given by

The velocity profile in fully developed laminar flow in a pipe of diameter $$D$$ is given by $$u = {u_0}\left( {1 - 4{r^2}/{D^2}} \right),$$ where $$r$$ is the radial distance from the center. If the viscosity of the fluid is $$\mu ,$$ the pressure drop across a length $$L$$ of the pipe is

A siphon draws water from a reservoir and discharges it out at atmospheric pressure. Assuming ideal fluid and the reservoir is large, the velocity at point $$P$$ in the siphon tube is:

A smooth flat plate with a sharp leading edge is placed along a gas stream flowing at $$U = 10\,m/s.$$ The thickness of the boundary layer at section $$r$$- $$s$$ is $$10$$ $$mm,$$ the breadth of the plate is $$1$$ $$m$$ (into the paper) and the density of the gas, $$\rho = 1.0\,kg/{m^3}.$$ Assume that the boundary layer is thin, two-dimensional, and follows a linear velocity distribution, $$u = U\left( {y/\delta } \right),$$ at the section $$r$$-$$s$$, where $$y$$ is the height from plate.

The mass flow rate (in kg/s) across the section $$q$$-$$r$$ is

A $$100$$ $$W$$ electric bulb was switched on in a $$2.5 \times 3 \times 3m$$ size thermally insulated room having temperature of $${20^0}C.$$ Room temp at the end of $$24$$ hours will be

With an increase in the thickness of insulation around a circular pipe, heat loss to surroundings due to

In a composite slab, the temperature at the interface (T_inter) between two materials is equal to the average of the temperatures at the two ends. Assuming steady one-dimensional heat conduction, which of the following statements is true about the respective thermal conductivities?

Consider the following data for an item.
Annual demand: $$2500$$ units per year Ordering cost: Rs.100 per order Inventory holding rate: $$25\% $$ of unit price. The optimum order quantity (in units) is:

Price quoted by a supplier

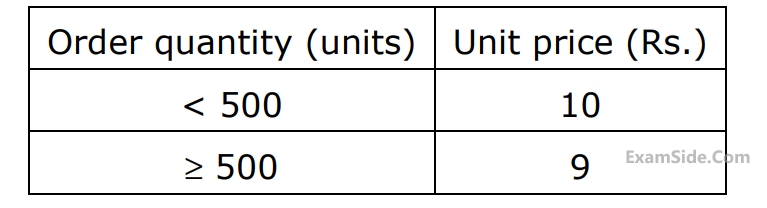
The optimum order quantity (in units) is

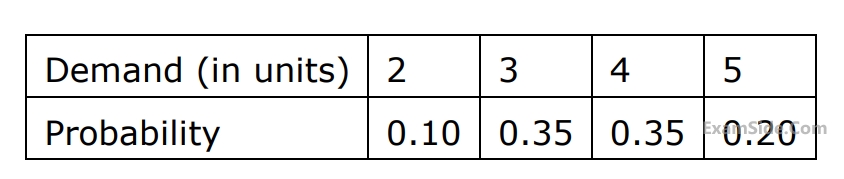A stockist wishes to optimize the number of perishable items he needs to stock in any month in his store. The demand distribution for this perishable item is: The stockist pays Rs.$$70$$ for each item and he sells each at Rs.$$90.$$ if the stock is left unsold in any month, he can sell the item at Rs.$$50$$ each. There is no penalty for unfulfilled demand. To maximize the expected profit, the optimal stock level is:

Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)

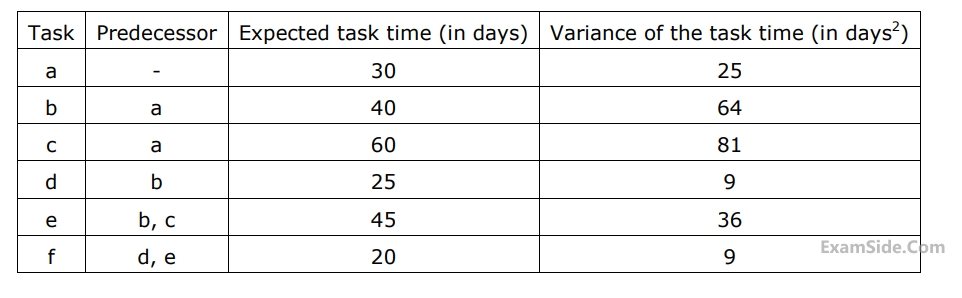
The expected completion time of the project is

Consider a $$PERT$$ network for a project involving six tasks ($$a$$ to $$f$$)

The standard deviation of the critical path of the project is

The table gives details of an assembly line.

What is the line efficiency of the assembly line?

The number of customers arriving at a railway reservation counter is Poisson distributed with an arrival rate of eight customers per hour. The reservation clerk at this counter takes six minutes per customer on an average with an exponentially distributed service time. The average number of the customers in the queue will be.

A firm is required to procure three items $$(P, Q$$ and $$R).$$ The prices quoted for these items (in Rs.) by suppliers $${S_1},{S_2},$$ and $${S_3}$$ are given in table. The management policy requires that each item has to be supplied by only one supplier and one supplier supply only one item. The minimum total cost (in Rs.) of procurement to the firm is:

A cylindrical shafts is subjected to an alternating stress of $$100MPa.$$ Fatigue strength to sustain $$1000$$ cycles is $$490MPa.$$ If the corrected endurance strength is $$70MPa,$$ estimated shaft life will be

A $$60mm$$ long and $$6mm$$ thick fillet weld carries a steady load of $$15kN$$ along the weld. The shear strength of the weld material is equal to $$200MPa.$$ The factor of safety is

Twenty degree full depth involute profiled $$19$$-tooth pinion and $$37$$-tooth gear are in mesh. If the module is $$5mm,$$ the center distance between the gear pair will be

A disk clutch is required to transmit $$5$$ $$kW$$ at $$2000$$ $$rpm$$ the disk has a friction lining with Coefficient of friction equal to $$0.25.$$ Bore radius of friction lining is equal to $$25mm.$$ Assume uniform contact pressure of $$1MPa.$$ The value of outside radius of the friction lining is

A $$4$$ $$mm$$ thick sheet is rolled with $$300$$ $$mm$$ diameter rolls to reduce thickness without any change in its width. The friction coefficient at the work-roll interface is $$0.1.$$ The minimum possible thickness of the sheet that can be produced in a single pass is

In a sand casting operation, the total liquid head is maintained constant such that it is equal to the mould height. The time taken to fill the mould with a top gate is $${t_A}.$$ If the same mould is filed with a bottom gate, then the time taken is $${t_B}.$$ Ignore the time required to fill the runner and frictional effects. Assume atmospheric pressure at the top molten metal surfaces. The relation between the $${t_A}$$ and $${t_B}$$ is

An expendable pattern is used in

In a wire drawing operation, diameter of a steel wire is reduced from $$10$$ $$mm$$ to $$8$$ $$mm.$$ the mean flow stress of the material is $$400$$ $$MPa.$$ The ideal force required for drawing ignoring friction and redundant work is:

In arc welding process, the voltage and current are $$25V$$ and $$300A$$ respectively. The arc heat transfer efficiency is $$0.85$$ and welding speed is $$8$$ $$mm/sec$$. The net heat input (in $$J/mm$$) is

In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory

The coefficient of friction at the tool chip interface is

In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory

The values of shear angle and shear strain, respectively are

In an orthogonal machining operation:
$$\,\,\,\,\,\,\,\,\,\,$$Uncut thickness $$\,\,\,\,\,$$ $$= 0.5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting speed $$\,\,\,\,\,\,\,\,\,\,$$ $$= 20$$ $$m/min$$
$$\,\,\,\,\,\,\,\,\,\,$$Width of cut $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 5$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$\,\,\,\,\,\,\,\,$$ $$= 0.7$$ $$mm$$
$$\,\,\,\,\,\,\,\,\,\,$$Thrust force$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Cutting force $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$= 1200$$ $$N$$
$$\,\,\,\,\,\,\,\,\,\,$$Rake angle $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$ = {15^ \circ }$$
Assume Merchant’s theory

The percentage of total energy dissipated due to friction at the tool chip interface is

If each abrasive grain is viewed as a cutting tool, then which of the following represents the cutting parameters in common grinding operations?

Match the items in column $${\rm I}$$ and $${\rm I}$$ $${\rm I}$$

Ring gage is used to measure

$$NC$$ contouring is an example of

A pin-ended column of length $$L,$$ modulus of elasticity $$E$$ and second moment of the cross-sectional area $$I$$ is loaded centrally by a compressive load $$P.$$ The critical buckling load $$\left( {{P_{cr}}} \right)$$ is given by

For a circular shaft of diameter $$'d'$$ subjected to torque $$T,$$ the maximum value of the shear stress is

A simply supported beam of span length $$6$$m and $$75$$ mm diameter carries a udl of $$1.5$$ kN/m

What is the maximum value of bending moment?

A simply supported beam of span length $$6$$m and $$75$$ mm diameter carries a udl of $$1.5$$ kN/m

What is the maximum value of bending stress?

A bar having a cross-sectional area of 700 mm² is subjected to axial loads at the positions indicated. The value of stress in the segment BC is

A steel bar of 40 mm × 40 mm square cross-section is subjected to an axial compressive load of 200 kN. If the length of the bar is 2m and E = 200 GPa. The decrement in length of the bar will be

The number of inversions for a slider crank mechanism is

A planetary gear train has four gears and one carrier. Angular velocities of the gears are $${\omega _1},{\omega _2},{\omega _3},$$ and $${\omega _4}$$ respectively. The carrier rotates with angular velocity $${\omega _5}.$$

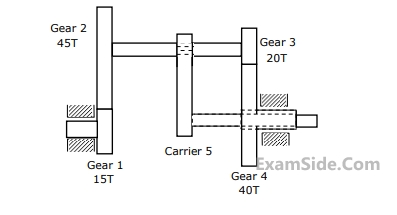
For $${{\omega _1} = 60}$$ rpm clockwise $$(CW)$$ when looked from the left, what is the angular velocity of the carrier and its direction so that Gear $$4$$ rotates in counter clockwise $$(CCW)$$ direction at twice the angular velocity of Gear $$1$$ when looked from the left?

A planetary gear train has four gears and one carrier. Angular velocities of the gears are $${\omega _1},{\omega _2},{\omega _3},$$ and $${\omega _4}$$ respectively. The carrier rotates with angular velocity $${\omega _5}.$$

What is the relation between the angular velocities of Gear $$1$$ and Gear $$4$$?

Match the items in columns $$I$$ and $$II$$

Column $$I$$
$$P.$$ Addendum
$$Q.$$ Instantaneous center of velocity
$$R.$$ Section modulus
$$S.$$ Prince circle

Column $$II$$
$$1.$$ Cam
$$2.$$ Beam
$$3.$$ Linkage
$$4.$$ Gear

In a four-bar linkage, $$S$$ denotes the shortest link length, $$L$$ is the longest link length, $$P$$ and $$Q$$ are the lengths of other two links. At least one of the three moving links will rotate by $${360^ \circ }$$ if

Match the items in column $$I$$ and $$II$$

List $$I$$
$$P.$$ Higher kinematic pair
$$Q.$$ Lower kinematic pair
$$R.$$ Quick return mechanism
$$S.$$ Mobility of a linkage

List $$II$$
$$1.$$ Grubler's equation
$$2.$$ Line contact
$$3.$$ Euler's equation
$$4.$$ planar
$$5.$$ Shaper
$$6.$$ Surface contact

For a four bar linkage in Toggle position, the value of mechanical advantage is

If $${C_f}$$ is the coefficient of speed fluctuation of a flywheel then the ratio of $${\omega _{\max }}/{\omega _{\min }}$$ will be

The differential equation governing the vibrating system is

A machine of $$250$$ kg mass is supported on springs of total stiffness $$100$$ kN/m. Machine has an unbalanced rotating force of $$350$$ N at speed of $$3600$$ rpm. Assuming a damping factor of $$0.15,$$ the value of transmissibility ratio is

A vibratory system consists of a mass $$12.5$$ kg, a spring of stiffness $$1000$$ $$N/m,$$ and a dashpot with damping coefficient of $$15$$ $$Ns/m.$$

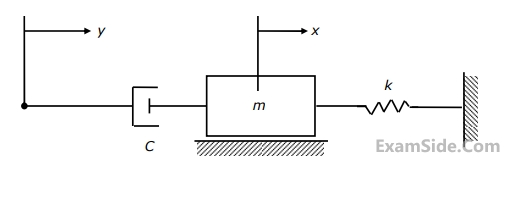
The value of logarithmic decrement is

A vibratory system consists of a mass $$12.5$$ kg, a spring of stiffness $$1000$$ $$N/m,$$ and a dashpot with damping coefficient of $$15$$ $$Ns/m.$$

The value of critical damping of the system is:

Match items from groups, $${\rm I},$$ $${\rm II},$$ $${\rm III},$$ $${\rm IV}$$ and $$V$$

Assertion (A): Condenser is an essential equipment in a steam power plant.

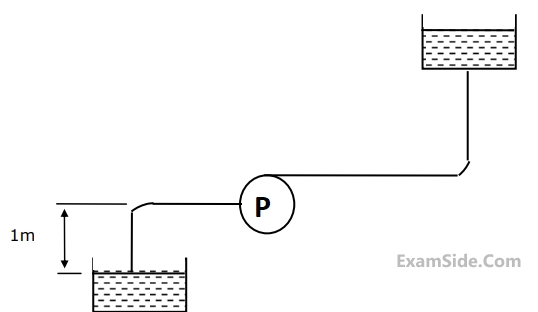
Reason(R): For the same mass flow rate and the same pressure rise, a water pump requires substantially less power than a steam compressor.

Determine the correctness or otherwise of the following Assertion $$(a)$$ and the Reason$$(r).$$

Assertion(A): In a power plant working on a Rankine cycle, the regenerative feed water heating improves the efficiency of the steam turbine.

Reason(R): The regenerative feed water heating raises the average temperature of heat addition in the Rankine cycle.

A $$100$$ $$W$$ electric bulb was switched on in a $$2.5\,m \times 3m \times 3m$$ size thermally insulated room having a temperature of $${20^ \circ }C$$. The room temperature at the end of $$24$$ hours will be

A football was inflated to a gauge pressure of $$1$$ bar when the ambient temperature was $${15^ \circ }C$$. When the game started next day, the air temperature at the stadium was $${5^ \circ }C$$.
Assume that the volume of the football remains constant at $$2500c{m^3}$$

Gauge pressure of air to which the ball must have been originally inflated so that it would equal $$1$$ bar gauge at the stadium is

A football was inflated to a gauge pressure of $$1$$ bar when the ambient temperature was $${15^ \circ }C$$. When the game started next day, the air temperature at the stadium was $${5^ \circ }C$$.
Assume that the volume of the football remains constant at $$2500c{m^3}$$

The amount of heat lost by the air in the football and the gauge pressure of air in the football at the stadium respectively equal

Given below is an extract from steam tables.

Specific enthalpy of water in $$kJ/kg$$ at $$150$$ bar and $$ {45^ \circ }C$$ is

A horizontal shaft centrifugal pump lifts ware at 65°C. The suction nozzle is one meter below pump centerline. The pressure at this point equal $$200$$ $$kPa$$ gauge and velocity is $$3$$ $$m/s.$$ Steam tables show saturation pressure at $${65^0}C$$ is $$25$$ $$kPa,$$ and specific volume of the saturated liquid is $$0.001020$$$ $${m^3}/kg.$$ . The pump Net Positive suction Head ($$NPSH$$) in meters is

A large hydraulic turbine is to generate $$300$$ $$kW$$ at $$1000$$ $$rpm$$ under a head of $$40$$ $$m$$. for initial testing, a $$1:4$$ scale model of the turbine operates under a head of $$10$$ $$m.$$ the power generated by the model (in $$kW$$) will be

In a Pelton wheel, the bucket peripheral speed is $$10$$ $$m/s,$$ the water jet velocity is $$25$$ $$m/s$$ and volumetric flow rate of the jet is $$0.1{m^3}/s.$$ If the jet deflection angle is $${120^0}$$ and the flow is ideal, the owe developed is: