The solution to the system of equations is $$\left[ {\matrix{ 2 & 5 \cr { - 4} & 3 \cr } } \right]\left\{ {\matrix{ x \cr y \cr } } \right\} = \left\{ {\matrix{ 2 \cr { - 30} \cr } } \right\}$$

Consider the function $$f\left( x \right) = 2{x^3} - 3{x^2}\,\,$$ in the domain $$\,\left[ { - 1,2} \right].$$ The global minimum of $$f(x)$$ is _________.

Consider a Poisson distribution for the tossing of a biased coin. The mean for this distribution is $$\mu $$.

The standard deviation for this distribution is given by

If $$y = f(x)$$ satiesfies the boundary value problem $$\,\,y''\,\,\, + \,\,\,9y\,\,\, = \,\,\,0,\,\,\,y\left( 0 \right)\,\,\, = \,\,\,0,\,$$ $$\,\,y\left( {{\pi \over 2}} \right) = \sqrt 2 ,\,\,\,$$ then $$\,\,y\left( {{\pi \over 4}} \right)\,\,$$ is _______.

Solve the equation $$x = 10\,\cos \,\left( x \right)$$ using the Newton-Raphson method. The initial guess is $$x = {\pi \over 4}.$$ The value of the predicted root after the first iteration, up to second decimal, is _____________.

Gauss-Seidel method is used to solve the following equations (as per the given order). $$${x_1} + 2{x_2} + 3{x_3} = 5$$$ $$$2{x_1} + 3{x_2} + {x_3} = 1$$$ $$$\,3{x_1} + 2{x_2} + {x_3} = 3$$$
Assuming initial guess as $${x_1} = {x_2} = {x_3} = 0,$$ the value of $${x_3}$$ after the first iteration is __________.

$$f\left( z \right) = u\left( {x,y} \right) + i\,\,\,\,v\left( {x,y} \right)$$ is an analytic function of complex variable $$z=x+iy$$ , where $$i = \sqrt { - 1} $$ If $$u(x,y)=2xy,$$ then $$v(x,y)$$ may be expressed as

The value of the integral $$\int\limits_{ - \infty }^\infty {{{\sin x} \over {{x^2} + 2x + 2}}} dx$$
evaluated using contour integration and the residue theorem is

A point mass $$M$$ is released from rest and slides down a spherical bowl (of radius $$R$$) from a height $$H$$ as shown in the figure below. The surface of the bowl is smooth (no friction). The velocity of the mass at the bottom of the bowl is

A block of mass m rests on an inclined plane and is attached by a string to the wall as shown in the figure. The coefficient of static friction between the plane and the block is $$0.25.$$ The string can withstand a maximum force of $$20$$ N. The maximum value of the mass (m) for which the string will not break and the block will be in static equilibrium is ____________ kg.
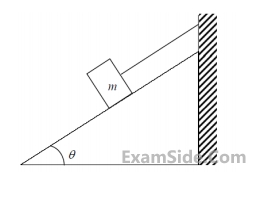
Take $$\cos \theta = 0.8$$ and $$\sin \theta = 0.6$$. Acceleration due to gravity g $$=$$ $$10$$ m/s²

A two-member truss $$PQR$$ is supporting a load W. The axial forces in members $$PQ$$ and $$QR$$ are respectively

A rigid ball of weight $$100$$ $$N$$ is suspended with the help of a string. The ball is pulled by a horizontal force $$F$$ such that the string makes an angle of $${30^0}$$ with the vertical. The magnitude of force $$F$$ (in N) is __________

The instantaneous stream-wise velocity of a turbulent flow is given as follows: $$$u\left( {x,y,z,t} \right) = \overline u \left( {x,y,z} \right) + \mu '\left( {x,y,z,t} \right)$$$

The time - average of the fluctuating velocity $$u'(x,y,z,t)$$

A steady laminar boundary layer is formed over a flat plate as shown in the figure. The free stream velocity of the fluid is $${U_0}.$$ The velocity profile at the inlet $$a$$-$$b$$ is uniform, while that at a downstream location $$c$$-$$d$$ is
given by $$u = {U_0}\left[ {2\left( {{y \over \delta }} \right) - {{\left( {{y \over \delta }} \right)}^2}} \right]$$

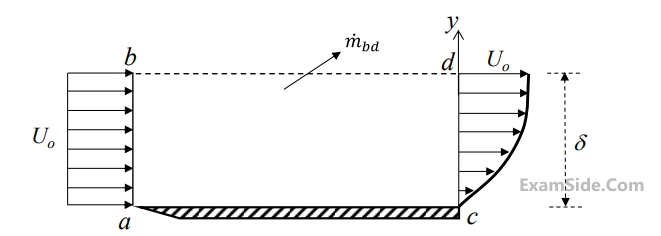
The ratio of the mass flow rate, $$\mathop {m{}_{bd}}\limits^ \bullet ,$$ leaving through the horizontal section $$b$$-$$d$$ to that entering through the vertical section $$a$$-$$b$$ is

An inverted U-tube manometer is used to measure the pressure difference between two pipes $$A$$ and $$B,$$ as shown in the figure. Pipe $$A$$ is carrying oil (specific gravity $$= 0.8$$) and pipe $$B$$ is carrying water. The densities of air and water are $$1.16\,\,kg/{m^3}$$ and $$1000\,\,kg/{m^3},$$, respectively. The pressure difference between pipes $$A$$ and $$B$$ is _______________$$kPa.$$

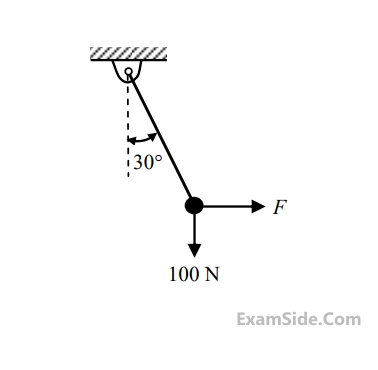
$$Acceleration$$ $$due$$ $$to$$ $$gravity$$ $$g = 10\,m/{s^2}$$

For a floating body, buoyant force acts at the

A plastic sleeve of outer radius $${r_0} = 1\,\,mm$$ covers a wire (radius $$r = 0.5$$ $$mm$$) carrying electric current. Thermal conductivity of the plastic is $$0.15\,\,W/m$$-$$K$$. The heat transfer coefficient on the outer surface of the sleeve exposed to air is $$25$$ $$W/{m^2}$$-$$K$$. Due to the addition of the plastic cover, the heat transfer from the wire to the ambient will

A steel ball of $$10$$ $$mm$$ diameter at $$1000$$ $$K$$ is required to be cooled to $$350$$ $$K$$ by immersing it in a water environment at $$300$$ $$K.$$ The convective heat transfer coefficient is $$1000\,\,W/{m^2}$$-$$K.$$ Thermal conductivity of steel is $$40$$ $$W/m$$-$$K.$$ The time constant for the cooling process $$\tau $$ is $$16s.$$ The time required (in $$s$$) to reach the final temperature is __________________.

An infinitely long furnace of $$0.5m \times 0.4m$$ cross-section is shown in the figure below. Consider all surfaces of the furnace to be black. The top and bottom walls are maintained at temperature $${T_1} = {T_3} = {927^ \circ }C,$$
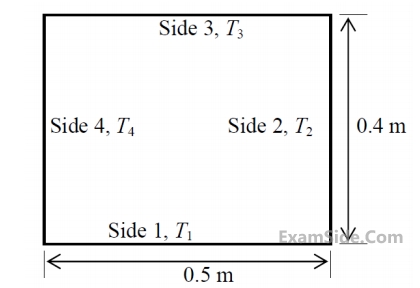
while the side walls are at temperature $${T_2} = {T_4} = {527^ \circ }C.$$
The view factor, $${F_{1 - 2}}$$ is $$0.26.$$ The net radiation heat loss or gain on side $$1$$ is_________ $$W/m.$$ Stefan-Boltzman constant $$ = \,5.67 \times {10^{ - 8}}$$ $$W/{m^2}$$-$${K^4}$$

A fluid (Prandtl number, $$Pr=1$$) at $$500$$ $$K$$ flows over a flat plate of $$1.5$$ $$m$$ length, maintained at $$300$$ $$K.$$ The velocity of the fluid is $$10\,\,m/s.$$ Assuming kinematic viscosity, $$v = 30 \times {10^{ - 6}}\,\,{m^2}/s,$$ the thermal boundary layer thickness (in $$mm$$) at $$0.5$$ $$m$$ from the leading edge is _________.

The annual demand for an item is $$10,000$$ units. The unit cost is Rs. $$100$$ and inventory carrying charges are $$14.4\% $$ of the unit cost per annum. The cost of one procurement is Rs. $$2000.$$ The time between two consecutive orders to meet the above demand is _______ month(s).

Maximize $$\,\,\,\,Z = 15{x_1} + 20{x_2}$$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$

The above linear programming problem has

The principal stresses at a point inside a solid object are $${\sigma _1} = 100\,\,MPa,\,\,{\sigma _2} = 100\,\,MPa$$ and $${\sigma _3} = 0\,\,MPa.$$ The yield strength of the material is $$200$$ $$MPa.$$ The factor of safety calculated using Tresca (maximum shear stress) theory is $${n_T}$$ and the factor of safety calculated using Von Mises (maximum distortional energy) theory is $${n_V}$$. Which one of the following relations is TRUE?

The part of a gating system which regulates the rate of pouring of molten metal is

Heat is removed from a molten metal of mass $$2$$ $$kg$$ at a constant rate of $$10$$ $$kW$$ till it is completely solidified. The cooling curve is shown in the figure.

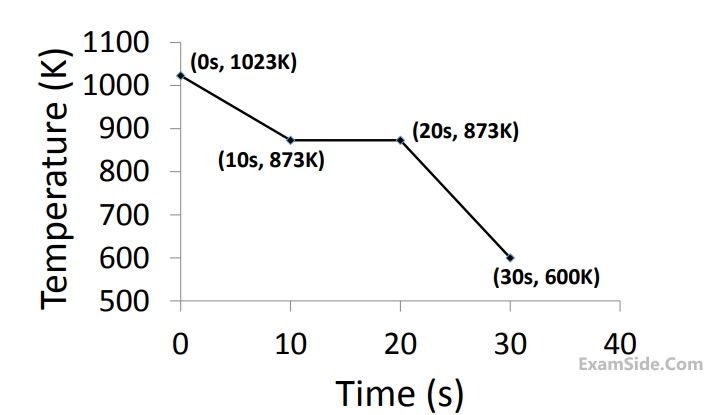
Assuming uniform temperature throughout the volume of the metal during solidification, the latent heat of fusion of the metal (in $$kJ/kg$$) is ______________

A cylindrical job with diameter of $$200$$ $$mm$$ and height of $$100$$ $$mm$$ is to be cast using modulus method of riser design. Assume that the bottom surface of cylindrical riser does not contribute as cooling surface. If the diameter of the riser is equal to its height, then the height of the riser (in $$mm$$) is

A $$300$$ $$mm$$ thick slab is being cold rolled ussing roll of $$600$$ $$mm$$ diameter. If the coefficient of friction is $$0.08,$$ the maximum possible reduction (in $$mm$$) is _______

A $$300$$ $$mm$$ thick slab is being cold rolled using roll of $$600$$ $$mm$$ diameter. If the coefficient of friction is $$0.08,$$ the maximum possible reduction (in $$mm$$) is _______________

Under optimal conditions of the process the temperatures experienced by a copper work piece in fusion welding, brazing and soldering are such that

In an orthogonal cutting process the tool used has rake angle of zero degree. The measured cutting force and thrust force are $$500$$ $$N$$ and $$250$$ $$N,$$ respectively. The coefficient of friction between the tool and the chip is ________________

The too life equation for $$HSS$$ tool is $$V{T^{0.14}}\,\,{f^{0.7}}\,\,{d^{0.4}} = $$ Constant. The tool life $$(T)$$ of $$30$$ $$min$$ is obtained using the following cutting conditions $$=45$$ $$m/min,$$ $$f=0.35mm,$$ $$d=2.0$$ $$mm.$$ If speed $$(V),$$ feed $$(f)$$ and depth of cut $$(D)$$ are increased individually by $$25\% ,$$ the tool life (in $$min$$) is

Match the following

The figure below represents a triangle $$PQR$$ with initial coordinates of the vertices as $$P(1,3),$$ $$Q(4,5)$$ and $$R(5,3.5).$$ The triangle is rotated in the $$X-Y$$ plane about the vertex $$P$$ by angle in clockwise direction. If sin $$\theta = 0.6$$ and cos $$\theta = 0.8$$, the new coordinates of the vertex $$Q$$ are

A horizontal bar with a constant cross-section is subjected to loading as shown in the figure. The Young’s modules for the sections AB and BC are 3E and E, respectively.
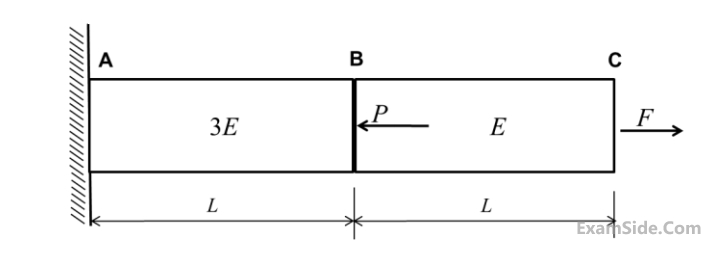
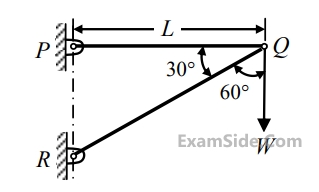
For the deflection at C to be zero, the ratio P/F is ________.

A hypothetical engineering stress-strain curve shown in the figure has three straight lines PQ, QR, RS with coordinates P(0,0), Q(0.2,100), R(0.6,140) and S(0.8,130). 'Q' is the yield point, 'R' is the UTS point and 'S' the fracture point.

The tougness of the material (in MJ/m³) is __________.

The figure shows cross-section of a beam subjected to bending. The area moment of inertia (in mm⁴) of this cross-section about its base is __________.

A simply-supported beam of length $$3L$$ is subjected to the loading shown in the figure.

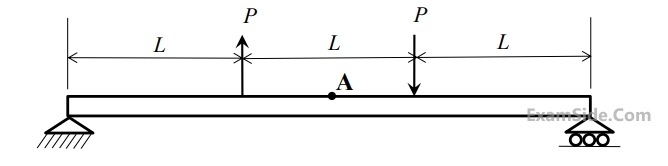
It is given that $$P = 1$$ $$N,$$ $$L = 1$$ $$m$$ and Young’s modulus $$E = 200$$ $$GP$$a. The cross-section is a square with dimension $$100$$ $$mm$$. The bending stress (in Pa) at the point A located at the top surface of the beam at a distance of $$1.5L$$ from the left end is _____________ .

(Indicate compressive stress by a negative sign and tensile stress by a positive sign).

The spring constant of a helical compression spring DOES NOT depend on

The cross sections of two hollow bars made of the same material are concentric circles as shown in the figure. It is given that 𝑟₃ > 𝑟₁ and 𝑟₄ > 𝑟₂ , and that the areas of the cross-sections are the same. J₁ and J₂ are the torsional rigidities of the bars on the left and right, respectively. The ratioJ₂/J₁ is

A cantilever beam having square cross-section of side $$a$$ is subjected to an end load. If a is increases by $$19$$%, the tip deflection decreases approximately by

In the gear train shown, gear 3 is carried on arm 5. Gear 3 meshes with gear 2 and gear 4. The number of teeth on gear 2, 3, and 4 are 60, 20, and 100, respectively. If gear 2 is fixed and gear rotates with an angular velocity of 100 rpm in the counterclockwise direction, the angular speed of arm 5 (in rpm) is

A single degree of freedom spring mass system with viscous damping has a spring constant of 10 kN/m. The system is excited by a sinusoidal force of amplitude 100 N. If the damping factor (ratio) is 0.25, the amplitude of steady state oscillation at resonance is ________mm.

A solid disc with radius a is connected to a spring at a point $$d$$ above the center of the disc. The other end of the spring is fixed to the vertical wall. The disc is free to roll without slipping on the ground. The mass of the disc is $$M$$ and the spring constant is $$K$$. The polar moment of inertia for the disc about its centre is $$J = {{M{a^2}} \over 2}$$

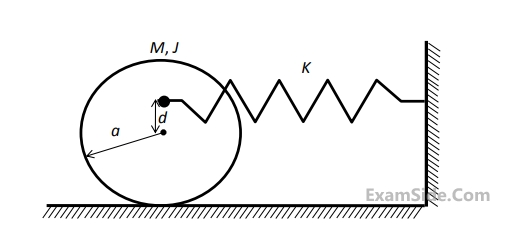
The natural frequency of this system in rad/s is given by

Which of the following statements are TRUE with respect to heat and work?
$$(i)$$ They are boundary phenomena
$$(ii)$$ They are exact differentials
$$(iii)$$ They are path functions

An ideal gas undergoes a reversible process in which the pressure varies linearly with volume. The conditions at the start (subscript $$1$$) and at the end (subscript $$2$$) of the process with usual notation are:
$${P_1} = 100\,\,kPa,\,\,{V_1} = 0.2\,{m^3}$$ and $${P_2} = 200\,\,kPa,\,\,{V_2} = 0.1\,{m^3}$$
and the gas constant, $$R = 0.275$$ $$kJ/kg$$-$$K.$$ The magnitude of the work required for the process (in $$kJ$$) is _______________

The INCORRECT statement about regeneration in vapor power cycle is that

In a steam power plant operating on an ideal Rankine cycle, super-heated steam enters the turbine at $$3$$ $$MPa$$ and $${350^ \circ }C.$$ The condenser pressure is $$75$$ $$kPa.$$ Thermal efficiency of the cycle is ___________ percent.

Given data:

For saturated liquid, at $$P=75$$ $$kPa,$$
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,{h_f} = 384.39\,\,kJ/kg, \cr & \,\,\,\,\,\,\,\,\,\,{v_f} = 0.001037\,\,{m^3}/kg, \cr & \,\,\,\,\,\,\,\,\,\,{s_f} = 1.213\,\,kJ/kg K \cr} $$

At $$75$$ $$kPa,$$ $${h_{fg}} = 2278.6\,\,kJ/kg,$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,{s_{fg}} = 6.2434\,\,kJ/kg$$-$$K$$

At $$P=3$$ $$MPa$$ and
$$\,\,\,\,\,\,\,\,\,\,T = {350^ \circ }C\,\,\,$$ (Superheated steam),
$$\,\,\,\,\,\,\,\,\,\,h = 3115.3\,\,kJ/kg,$$
$$\,\,\,\,\,\,\,\,\,\,s = 6.7428\,\,kJ/kg$$-$$K$$

Consider two hydraulic turbines having identical specific speed and effective head at the inlet. If the speed ratio $$\left( {{{{N_1}} \over {{N_2}}}} \right)$$ of the two turbines is $$2,$$ then the respective power ratio $$\left( {{{{P_1}} \over {{P_2}}}} \right)$$ is _______________________.