GATE ME
$$V = \left( {{a_1}x + {a_2}y + {a_3}z} \right)i + \left( {{b_1}x + {b_2}y + {b_3}z} \right)j\,$$ $$ + \left( {{c_1}x + {c_2}y + {c_3}z} \right)k,\,\,$$
where $${{a_1} = 2}$$ and $${{c_3} = - 4.}$$ The value of $${{b_2}}$$ is ________.
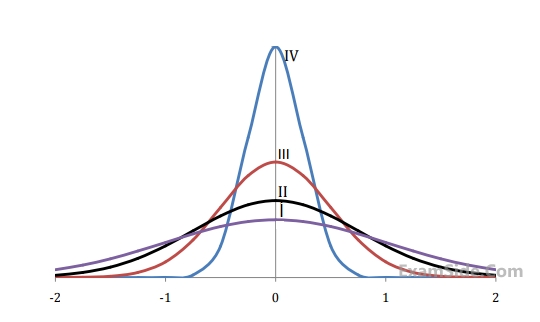
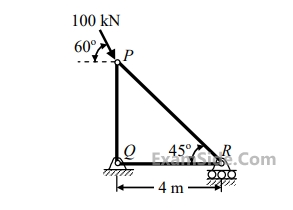
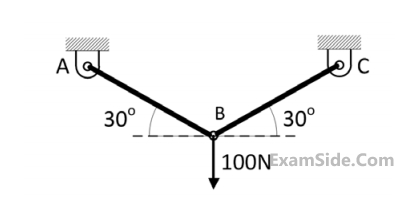

$$V = \left( {{a_1}x + {a_2}y + {a_3}z} \right)i + \left( {{b_1}x + {b_2}y + {b_3}z} \right)j$$ $$$ + \left( {{c_1}x + {c_2}y + {c_3}z} \right)k,$$$
Where $${a_1} = 2$$ and $${c_3} = - 4.$$ The value of $${b_2}$$ is _____________.
$$U\left( {r,x} \right) = {C_1}$$ and $$T\left( {r,x} \right) = {C_2}\left[ {1 - {{\left( {{r \over R}} \right)}^3}} \right],$$
where $${C_1}$$ and $${C_2}$$ are constants. The bulk mean temperature is given by
$${T_m} = {2 \over {{U_m}{R^2}}}\int\limits_0^R {u\left( {r,x} \right)T\left( {r,x} \right)rdr,} $$
with $${{U_m}}$$ being the mean velocity of flow. The value of $${T_m}$$ is
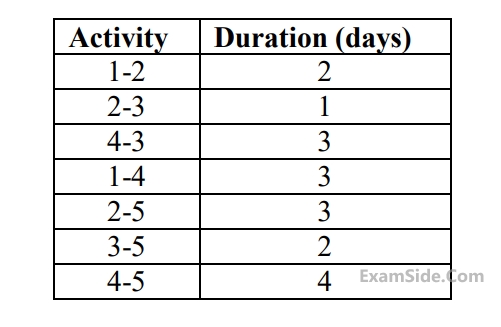
The critical path $$(CP)$$ in the network is
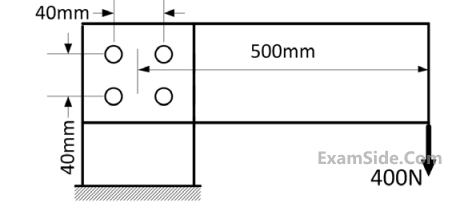
The minimum clearance in the assembly will be
$$\eqalign{ & {L_1} = {22.0^{ \pm 0.01}}\,\,mm, \cr & {L_2} = {L_3} = {10.0^{ \pm 0.005}}\,\,mm, \cr} $$
Assuming the normal distributions of part dimensions, the dimension $${L_4}$$ in $$mm$$ for assembly condition would be,
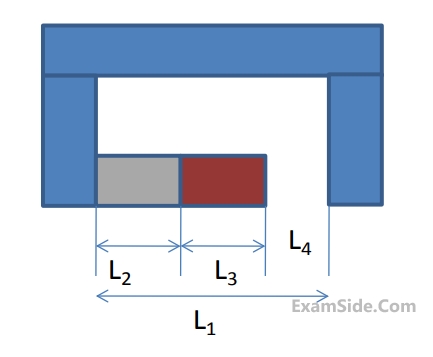
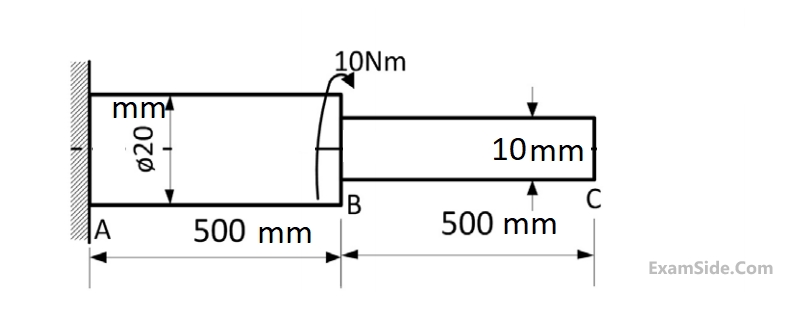

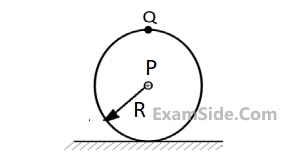
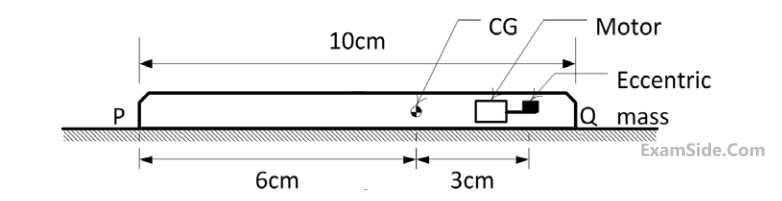
Given in addition that the eccentric mass = $$2$$ grams, eccentricity = $$2.19$$ mm, mass of the mobile = $$90$$ grams, g = $$9.81$$ $$m/{s^2}.$$ Uniform speed of the motor in $$RPM$$ for which the mobile will get just lifted off the ground at the end $$Q$$ is approximately
Intermediate stage: $$h=2776$$ $$kJ/kg$$
Exit of turbine : $$P=9kPa,$$ $${h_f} = 174\,\,kJ/kg,$$
$$\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{h_g} = 2574\,\,kJ/kg,\,\,\,{s_f} = 0.6kJ/\left( {kg.K} \right); \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,{s_g} = 8.1\,\,kJ/(kg.K) \cr} $$
If the flow rate of steam entering the turbine is $$100$$ $$kg/s,$$ then the work output (in $$MW$$) is __________.