A machine produces a defective component with a probability of 0.015. The number of defective components in a packed box containing 200 components produced by the machine follows a Poisson distribution. The mean and the variance of the distribution are

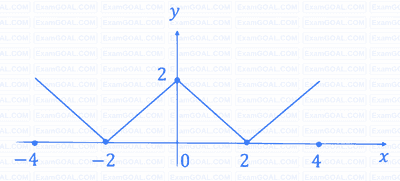
The figure shows the plot of a function over the interval [-4, 4]. Which one of the options given CORRECTLY identifies the function?

A vector field

𝐁(𝑥, 𝑦, 𝑧) = 𝑥 𝑖̂ + 𝑦 ĵ − 2𝑧 k̂

is defined over a conical region having height ℎ = 2, base radius 𝑟 = 3 and axis along z, as shown in the figure. The base of the cone lies in the x-y plane and is centered at the origin.

If 𝒏 denotes the unit outward normal to the curved surface 𝑆 of the cone, the value of the integral

$\rm \int_SB.n\ dS$

equals _________ . (Answer in integer)

A linear transformation maps a point (𝑥, 𝑦) in the plane to the point (𝑥̂, 𝑦̂) according to the rule

𝑥̂ = 3𝑦, 𝑦̂ = 2𝑥.

Then, the disc 𝑥² + 𝑦² ≤ 1 gets transformed to a region with an area equal to _________ . (Rounded off to two decimals)

Use π = 3.14. 

The value of k that makes the complex-valued function

𝑓(𝑧) = 𝑒−𝑘𝑥 (cos 2𝑦 − 𝑖 sin 2𝑦)

analytic, where 𝑧 = 𝑥 + 𝑖𝑦, is _________.

(Answer in integer)

Which one of the options given is the inverse Laplace transform of $\rm \frac{1}{s^3-s}$? 𝑢(𝑡) denotes the unit-step function.

The smallest perimeter that a rectangle with area of 4 square units can have is ______ units.

(Answer in integer)

Consider the second-order linear ordinary differential equation

$\rm x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx}-y=0, x\ge1$

with the initial conditions 

$\rm y(x=1)=6, \left.\frac{dy}{dx}\right|_{x=1}=2$

The value of 𝑦 at 𝑥 = 2 equals ________.

(Answer in integer)

The initial value problem

$\rm \frac{dy}{dt}+2y=0, y(0)=1$

is solved numerically using the forward Euler’s method with a constant and positive time step of Δt. 

Let 𝑦_𝑛 represent the numerical solution obtained after 𝑛 steps. The condition |𝑦_n+1| ≤ |𝑦_n| is satisfied if and only if Δt does not exceed _____________.

(Answer in integer)

The options show frames consisting of rigid bars connected by pin joints. Which one of the frames is non-rigid? 

A spherical ball weighing 2 kg is dropped from a height of 4.9 m onto an immovable rigid block as shown in the figure. If the collision is perfectly elastic, what is the momentum vector of the ball (in kg m/s) just after impact?

Take the acceleration due to gravity to be 𝑔 = 9.8 m/s². Options have been rounded off to one decimal place.

Air (density = 1.2 kg/m³, kinematic viscosity = 1.5 × 10^-5 m²/s) flows over a flat plate with a free-stream velocity of 2 m/s. The wall shear stress at a location 15 mm from the leading edge is τ_w. What is the wall shear stress at a location 30 mm from the leading edge?

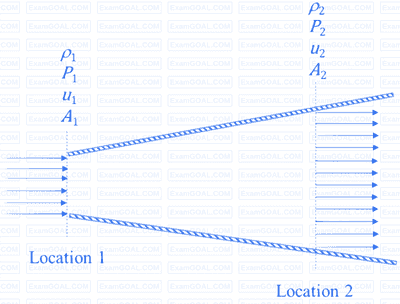
Consider an isentropic flow of air (ratio of specific heats = 1.4) through a duct as shown in the figure.

The variations in the flow across the cross-section are negligible. The flow conditions at Location 1 are given as follows:

𝑃₁ = 100 kPa, 𝜌₁ = 1.2 kg/m³ , 𝑢₁= 400 m/s

The duct cross-sectional area at Location 2 is given by A₂ = 2A₁, where A₁ denotes the duct cross-sectional area at Location 1. Which one of the given statements about the velocity 𝑢₂ and pressure 𝑃₂ at Location 2 is TRUE? 

The velocity field of a certain two-dimensional flow is given by

V(𝑥, 𝑦) = 𝑘(𝑥𝑖̂ − 𝑦𝑗̂)

where 𝑘 = 2 s^-1. The coordinates 𝑥 and 𝑦 are in meters. Assume gravitational effects to be negligible.

If the density of the fluid is 1000 kg/m³ and the pressure at the origin is 100 kPa, the pressure at the location (2 m, 2 m) is _____________ kPa.

(Answer in integer)

Consider a unidirectional fluid flow with the velocity field given by

V(𝑥, 𝑦, 𝑧, 𝑡) = 𝑢(𝑥, 𝑡) 𝑖̂

where 𝑢(0,𝑡) = 1. If the spatially homogeneous density field varies with time 𝑡 as

𝜌(𝑡) = 1 + 0.2𝑒^−𝑡

the value of 𝑢(2, 1) is ______________. (Rounded off to two decimal places) Assume all quantities to be dimensionless.

The figure shows two fluids held by a hinged gate. The atmospheric pressure is P_a = 100 kPa. The moment per unit width about the base of the hinge is ____________ kNm/m. (Rounded off to one decimal place)

Take the acceleration due to gravity to be g = 9.8 m/s².

An explosion at time t = 0 releases energy 𝐸 at the origin in a space filled with a gas of density ρ. Subsequently, a hemispherical blast wave propagates radially outwards as shown in the figure.

Let R denote the radius of the front of the hemispherical blast wave. The radius R follows the relationship 𝑅 = 𝑘 𝑡^𝑎 𝐸 ^𝑏 𝜌^𝑐, where k is a dimensionless constant. The value of exponent a is ___________.

(Rounded off to one decimal place)

Consider incompressible laminar flow of a constant property Newtonian fluid in an isothermal circular tube. The flow is steady with fully-developed temperature and velocity profiles. The Nusselt number for this flow depends on

Consider a counter-flow heat exchanger with the inlet temperatures of two fluids (1 and 2) being T_{1, in} = 300 K and T_{2, in} = 350 K. The heat capacity rates of the two fluids are C₁ = 1000 W/K and C₂ = 400 W/K, and the effectiveness of the heat exchanger is 0.5. The actual heat transfer rate is _____ kW.

(Answer in integer)

A cylindrical rod of length ℎ and diameter 𝑑 is placed inside a cubic enclosure of side length 𝐿. 𝑆 denotes the inner surface of the cube.

The view-factor F_S-S is 

A very large metal plate of thickness 𝑑 and thermal conductivity 𝑘 is cooled by a stream of air at temperature 𝑇∞ = 300 K with a heat transfer coefficient ℎ, as shown in the figure. The centerline temperature of the plate is TP. In which of the following case(s) can the lumped parameter model be used to study the heat transfer in the metal plate? 

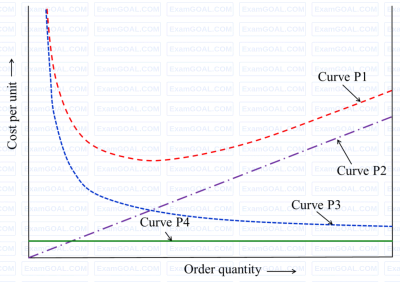
With reference to the Economic Order Quantity (EOQ) model, which one of the options given is correct? 

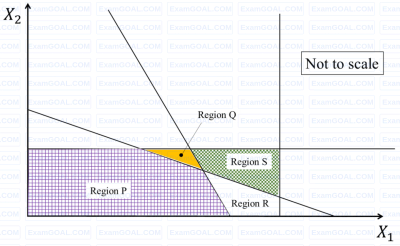
Which one of the options given represents the feasible region of the linear programming model:

𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 45𝑋₁ + 60𝑋₂

𝑋₁ ≤ 45

𝑋₂ ≤ 50

10𝑋₁ + 10𝑋₂ ≥ 600

25𝑋₁ + 5𝑋₂ ≤ 750

A solid part (see figure) of polymer material is to be fabricated by additive manufacturing (AM) in square-shaped layers starting from the bottom of the part working upwards. The nozzle diameter of the AM machine is a/10 mm and the nozzle follows a linear serpentine path parallel to the sides of the square layers with a feed rate of a/5 mm/min.

Ignore any tool path motions other than those involved in adding material, and any other delays between layers or the serpentine scan lines.

The time taken to fabricate this part is ___________ minutes.

(Answer in integer)

The S-N curve from a fatigue test for steel is shown. Which one of the options gives the endurance limit?

The braking system shown in the figure uses a belt to slow down a pulley rotating in the clockwise direction by the application of a force P. The belt wraps around the pulley over an angle α = 270 degrees. The coefficient of friction between the belt and the pulley is 0.3. The influence of centrifugal forces on the belt is negligible.

During braking, the ratio of the tensions T₁ to T₂ in the belt is equal to __________. (Rounded off to two decimal places)

Take π = 3.14.

In an ideal orthogonal cutting experiment (see figure), the cutting speed V is 1 m/s, the rake angle of the tool α = 5°, and the shear angle, 𝜙, is known to be 45°.

Applying the ideal orthogonal cutting model, consider two shear planes PQ and RS close to each other. As they approach the thin shear zone (shown as a thick line in the figure), plane RS gets sheared with respect to PQ (point R1 shears to R2, and S1 shears to S2).

Assuming that the perpendicular distance between PQ and RS is 𝛿 = 25 μm, what is the value of shear strain rate (in s^-1 ) that the material undergoes at the shear zone?

A CNC machine has one of its linear positioning axes as shown in the figure, consisting of a motor rotating a lead screw, which in turn moves a nut horizontally on which a table is mounted. The motor moves in discrete rotational steps of 50 steps per revolution. The pitch of the screw is 5 mm and the total horizontal traverse length of the table is 100 mm. What is the total number of controllable locations at which the table can be positioned on this axis?

The atomic radius of a hypothetical face-centered cubic (FCC) metal is (√2/10) nm. The atomic weight of the metal is 24.092 g/mol. Taking Avogadro’s number to be 6.023 × 10²³ atoms/mol, the density of the metal is ____________ kg/m³ .

(Answer in integer)

A steel sample with 1.5 wt.% carbon (no other alloying elements present) is slowly cooled from 1100 °C to just below the eutectoid temperature (723 °C). A part of the iron-cementite phase diagram is shown in the figure. The ratio of the pro-eutectoid cementite content to the total cementite content in the microstructure that develops just below the eutectoid temperature is ________.

(Rounded off to two decimal places)

A part, produced in high volumes, is dimensioned as shown. The machining process making this part is known to be statistically in control based on sampling data. The sampling data shows that D1 follows a normal distribution with a mean of 20 mm and a standard deviation of 0.3 mm, while D2 follows a normal distribution with a mean of 35 mm and a standard deviation of 0.4 mm. An inspection of dimension C is carried out in a sufficiently large number of parts.

To be considered under six-sigma process control, the upper limit of dimension C should be ____________ mm.

(Rounded off to one decimal place)

A coordinate measuring machine (CMM) is used to determine the distance between Surface SP and Surface SQ of an approximately cuboidal shaped part. Surface SP is declared as the datum as per the engineering drawing used for manufacturing this part. The CMM is used to measure four points P1, P2, P3, P4 on Surface SP, and four points Q1, Q2, Q3, Q4 on Surface SQ as shown. A regression procedure is used to fit the necessary planes.

The distance between the two fitted planes is ___________ mm.

(Answer in integer)

An optical flat is used to measure the height difference between a reference slip gauge A and a slip gauge B. Upon viewing via the optical flat using a monochromatic light of wavelength 0.5 µm, 12 fringes were observed over a length of 15 mm of gauge B. If the gauges are placed 45 mm apart, the height difference of the gauges is ______________ μm.

(Answer in integer)

The effective stiffness of a cantilever beam of length L and flexural rigidity EI subjected to a transverse tip load W is

A beam is undergoing pure bending as shown in the figure. The stress (𝜎)-strain (𝜀) curve for the material is also given. The yield stress of the material is 𝜎𝑌. Which of the option(s) given represent(s) the bending stress distribution at cross-section AA after plastic yielding? 

Which of the plot(s) shown is/are valid Mohr’s circle representations of a plane stress state in a material? (The center of each circle is indicated by O.)

A beam of length 𝐿 is loaded in the 𝑥𝑦 −plane by a uniformly distributed load, and by a concentrated tip load parallel to the 𝑧 −axis, as shown in the figure. The resulting bending moment distributions about the 𝑦 and the 𝑧 axes are denoted by 𝑀_𝑦 and 𝑀_𝑧 , respectively.

Which one of the options given depicts qualitatively CORRECT variations of 𝑀_𝑦 and 𝑀_𝑧 along the length of the beam?

The figure shows a thin-walled open-top cylindrical vessel of radius 𝑟 and wall thickness 𝑡. The vessel is held along the brim and contains a constant-density liquid to height ℎ from the base. Neglect atmospheric pressure, the weight of the vessel and bending stresses in the vessel walls.

Which one of the plots depicts qualitatively CORRECT dependence of the magnitudes of axial wall stress (σ₁) and circumferential wall stress (σ₂) on 𝑦? 

Cylindrical bars P and Q have identical lengths and radii, but are composed of different linear elastic materials. The Young’s modulus and coefficient of thermal expansion of Q are twice the corresponding values of P. Assume the bars to be perfectly bonded at the interface, and their weights to be negligible.

The bars are held between rigid supports as shown in the figure and the temperature is raised by Δ𝑇. Assume that the stress in each bar is homogeneous and uniaxial. Denote the magnitudes of stress in P and Q by σ1 and σ2, respectively.

Which of the statement(s) given is/are CORRECT?

Ignoring the small elastic region, the true stress (𝜎) – true strain (𝜀) variation of a material beyond yielding follows the equation 𝜎 = 400𝜀^0.3 MPa. The engineering ultimate tensile strength value of this material is ________ MPa.

(Rounded off to one decimal place)

The area moment of inertia about the y-axis of a linearly tapered section shown in the figure is _____________ m⁴ .

(Answer in integer)

A cylindrical bar has a length 𝐿 = 5 𝑚 and cross section area 𝑆 = 10 𝑚² . The bar is made of a linear elastic material with a density ρ = 2700 kg/m³ and Young’s modulus E = 70 GPa. The bar is suspended as shown in the figure and is in a state of uniaxial tension due to its self-weight.

The elastic strain energy stored in the bar equals _________ J. (Rounded off to two decimal places)

Take the acceleration due to gravity as 𝑔 = 9.8 m/s².

A cylindrical transmission shaft of length 1.5 m and diameter 100 mm is made of a linear elastic material with a shear modulus of 80 GPa. While operating at 500 rpm, the angle of twist across its length is found to be 0.5 degrees.

The power transmitted by the shaft at this speed is _______kW. (Rounded off to two decimal places)

Take π = 3.14.

A cuboidal part has to be accurately positioned first, arresting six degrees of freedom and then clamped in a fixture, to be used for machining. Locating pins in the form of cylinders with hemi-spherical tips are to be placed on the fixture for positioning. Four different configurations of locating pins are proposed as shown. Which one of the options given is correct?

Two meshing spur gears 1 and 2 with diametral pitch of 8 teeth per mm and an angular velocity ratio |ω2 |/|ω1 | = 1/4, have their centers 30 mm apart. The number of teeth on the driver (gear 1) is _______ .

(Answer in integer)

The figure shows a block of mass m = 20 kg attached to a pair of identical linear springs, each having a spring constant k = 1000 N/m. The block oscillates on a frictionless horizontal surface. Assuming free vibrations, the time taken by the block to complete ten oscillations is _________ seconds. (Rounded off to two decimal places)

Take π = 3.14.

The figure shows a wheel rolling without slipping on a horizontal plane with angular velocity 𝜔₁. A rigid bar PQ is pinned to the wheel at P while the end Q slides on the floor.

What is the angular velocity 𝜔₂ of the bar PQ?

A heat engine extracts heat (𝑄_H) from a thermal reservoir at a temperature of 1000 K and rejects heat (𝑄_L) to a thermal reservoir at a temperature of 100 K, while producing work (𝑊). Which one of the combinations of [𝑄_H, 𝑄_L and 𝑊] given is allowed? 

Which one of the following statements is FALSE?

Consider a fully adiabatic piston-cylinder arrangement as shown in the figure. The piston is massless and cross-sectional area of the cylinder is 𝐴. The fluid inside the cylinder is air (considered as a perfect gas), with γ being the ratio of the specific heat at constant pressure to the specific heat at constant volume for air. The piston is initially located at a position 𝐿1. The initial pressure of the air inside the cylinder is 𝑃₁ ≫ 𝑃₀, where 𝑃₀ is the atmospheric pressure. The stop S₁ is instantaneously removed and the piston moves to the position 𝐿₂, where the
equilibrium pressure of air inside the cylinder is 𝑃₂ ≫ 𝑃₀.

What is the work done by the piston on the atmosphere during this process?

Consider a mixture of two ideal gases, X and Y, with molar masses M̅_X = 10 kg/kmol and M̅_Y = 20 kg/kmol, respectively, in a container. The total pressure in the container is 100 kPa, the total volume of the container is 10 m³ and the temperature of the contents of the container is 300 K. If the mass of gas-X in the container is 2 kg, then the mass of gas-Y in the container is ____ kg. (Rounded off to one decimal place)

Assume that the universal gas constant is 8314 J kmol^-1K^-1.

He did not manage to fix the car himself, so he _______ in the garage.

Planting : Seed :: Raising : _____

(By word meaning) 

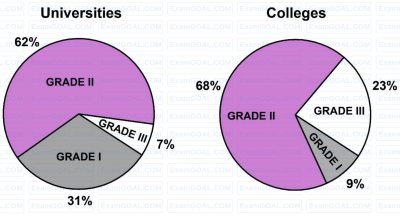
A certain country has 504 universities and 25951 colleges. These are categorised into Grades I, II, and III as shown in the given pie charts.

What is the percentage, correct to one decimal place, of higher education institutions (colleges and universities) that fall into Grade III? 

The minute-hand and second-hand of a clock cross each other _______ times between 09:15:00 AM and 09:45:00 AM on a day. 

The symbols O$, *, \Delta$, and $\square$ are to be filled, one in each box, as shown below.

The rules for filling in the four symbols are as follows.

1) Every row and every column must contain each of the four symbols.

2) Every 2 × 2 square delineated by bold lines must contain each of the four symbols.

Which symbol will occupy the box marked with ‘?’ in the partially filled figure?

In a recently held parent-teacher meeting, the teachers had very few complaints about Ravi. After all, Ravi was a hardworking and kind student. Incidentally, almost all of Ravi’s friends at school were hardworking and kind too. But the teachers drew attention to Ravi’s complete lack of interest in sports. The teachers believed that, along with some of his friends who showed similar disinterest in sports, Ravi needed to engage in some sports for his overall development.

Based only on the information provided above, which one of the following statements can be logically inferred with certainty?

Consider the following inequalities

𝑝² − 4𝑞 < 4

3𝑝 + 2𝑞 < 6

where 𝑝 and 𝑞 are positive integers.

The value of (𝑝 + 𝑞) is _______. 

Which one of the sentence sequences in the given options creates a coherent narrative?

(i) I could not bring myself to knock.

(ii) There was a murmur of unfamiliar voices coming from the big drawing room and the door was firmly shut.

(iii) The passage was dark for a bit, but then it suddenly opened into a bright kitchen.

(iv) I decided I would rather wander down the passage.

How many pairs of sets (S,T) are possible among the subsets of {1, 2, 3, 4, 5, 6} that satisfy the condition that S is a subset of T? 

An opaque pyramid (shown below), with a square base and isosceles faces, is suspended in the path of a parallel beam of light, such that its shadow is cast on a screen oriented perpendicular to the direction of the light beam. The pyramid can be reoriented in any direction within the light beam. Under these conditions, which one of the shadows P, Q, R, and S is NOT possible?