The function $$f(t)$$ satisfies the differential equation $${{{d^2}f} \over {d{t^2}}} + f = 0$$ and the auxiliary conditions, $$f\left( 0 \right) = 0,\,{{df} \over {dt}}\left( 0 \right) = 4.$$ The laplace transform of $$f(t)$$ is given by

Let $$X$$ be a normal random variable with mean $$1$$ and variance $$4.$$ The probability $$P\left\{ {X < 0} \right\}$$ is

The eigen values of a symmetric matrix are all

Choose the CORRECT set of functions, which are linearly dependent.

The value of the definite integral $$\int_1^e {\sqrt x \ln \left( x \right)dx} $$ is

The following surface integral is to be evaluated over a sphere for the given steady velocity vector field $$F = xi + yj + zk$$ defined with respect to a Cartesian coordinate system having $$i, j$$ and $$k$$ as unit base vectors. $$$\int {\int\limits_S {{1 \over 4}\left( {F.n} \right)dA} } $$$

Where $$S$$ is the sphere, $$\,\,{x^2} + {y^2} + {z^2} = 1\,\,$$ and $$n$$ is the outward unit normal vector to the sphere. The value of the surface integral is

The probability that a student knows the correct answer to a multiple choice question is $${2 \over 3}$$. If the student does not know the answer, then the student guesses the answer. The probability of the guessed answer being correct is $${1 \over 4}$$. Given that the student has answered the question correctly, the conditional probability that the student knows the correct answer is

The solution to the differential equation $$\,{{{d^2}u} \over {d{x^2}}} - k{{du} \over {dx}} = 0\,\,\,$$ where $$'k'$$ is a constant, subjected to the boundary conditions $$\,\,u\left( 0 \right) = 0\,\,$$ and $$\,\,\,u\left( L \right) = U,\,\,$$ is

The partial differential equation $$\,\,{{\partial u} \over {\partial t}} + u{{\partial u} \over {\partial x}} = {{{\partial ^2}u} \over {\partial {x^2}}}\,\,\,$$ is a

Match the CORRECT pairs.

A pin jointed uniform rigid rod of weight W and length is supported horizontally by an external force F as shown in the figure below. The force F is suddenly removed. At the instant of force removal, the magnitude of vertical reaction developed at the support is

For steady, fully developed flow inside a straight pipe of diameter $$D,$$ neglecting gravity effects, the pressure drop $$\Delta p$$ over a length $$L$$ and the wall shear stress $${\tau _w}$$ are related by

Water is coming out from a tap and falls vertically downwards. At the tap opening, the stream diameter is $$20$$ $$mm$$ with uniform velocity of $$2$$ $$m/s.$$ Acceleration due to gravity is $$9.81$$ $$m/{s^2}.$$ Assuming steady, inviscid flow, constant atmospheric pressure everywhere and neglecting curvature and surface tension effects, the diameter in mm of the stream $$0.5$$ $$m$$ below the tap is approximately

A hinged gate of length $$5$$ $$m,$$ inclined at $${30^ \circ }$$ with the horizontal and with water mass on its left, is shown in the figure below. Density of water is $$1000$$ $$kg/{m^3}$$. The minimum mass of the gate in kg per unit width (perpendicular to the plane of paper), required to keep it closed is

Consider one-dimensional steady state heat conduction, without heat generation, in a plane wall; with boundary conditions as shown in the figure below. The conductivity of the wall is given by $$k = {k_0} + bT;$$ where $${k_0}$$ and $$b$$ are positive constants, and $$T$$ is temperature.

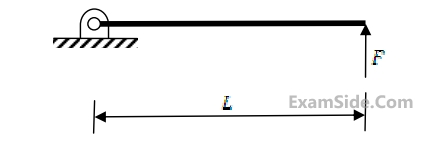
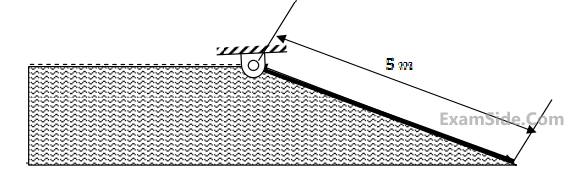
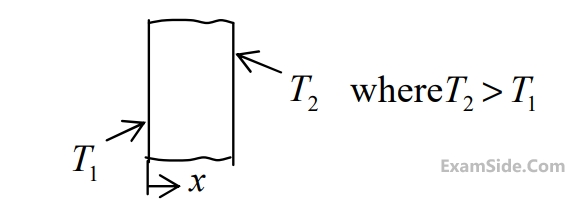
As $$x$$ increases, the state temperature gradient $$(dT/dx)$$ will

Consider one-dimensional steady state heat conduction along x-axis $$\left( {0 \le x \le L} \right),$$ through a planewall with the boundary surfaces $$(x=0$$ and $$x=L)$$ maintained at temperatures of $${0^ \circ }C$$ and $${100^ \circ }C$$. Heat is generated uniformly throughout the wall. Choose the CORRECT statement.

A steel ball of diameter $$60$$ $$mm$$ is initially in thermal equilibrium at $${1030^ \circ }C$$ in a furnace. It is suddenly removed from the furnace and cooled in ambient air at $${30^ \circ }C$$ with convective heat transfer coefficient $$h = 20\,W/{m^2}K.$$ The thermo-physical properties of steel are: density $$\rho = 7800\,\,kg/{m^3},$$ , conductivity $$k = 40 W/mK$$ and specific heat $$c = 600 J/kgK.$$ The time required in seconds to cool the steel ball in air from $${1030^ \circ }C$$ to $${430^ \circ }C$$ is

Two large diffuse gray parallel plates, separated by a small distance, have surface temperatures of $$400$$ $$K$$ and $$300$$ $$K.$$ If the emissivities of the surfaces are $$0.8$$ and the Stefan-Boltzmann constant is $$5.67 \times {10^{ - 8}}$$ $$W/{m^2}{K^4},$$ the net radiation heat exchange rate in $$kW/{m^2}$$ between the two plates is

Water (specific heat, $${c_p} = 4.18\,\,kJ/kgK$$ ) enters a pipe at a rate of $$0.01$$ $$kg/s$$ and temperature of $${20^ \circ }C.$$ The pipe, of diameter $$50$$ $$mm$$ and length $$3$$ $$m,$$ is subjected to a wall heat flux $${q_w}$$ in $$W/{m^2}:$$

If $${q_w}$$ $$=5000$$ and the convection heat transfer coefficient at the pipe outlet is $$1000$$ $$W/{m^2}K,$$ the temperature in $$^ \circ C$$ at the inner surface of the pipe at the outlet is

Water (specific heat, $${c_p} = 4.18\,\,kJ/kgK$$ ) enters a pipe at a rate of $$0.01$$ $$kg/s$$ and temperature of $${20^ \circ }C.$$ The pipe, of diameter $$50$$ $$mm$$ and length $$3$$ $$m,$$ is subjected to a wall heat flux $${q_w}$$ in $$W/{m^2}:$$

If $${q_w}$$ $$=2500x,$$ where $$x$$ is $$m$$ and in the direction of flow ($$x=0$$ at the inlet), the bulk mean temperature of the water leaving the pipe in $$^ \circ C$$ is

In simple exponential smoothing forecasting, to give higher weightage to recent demand information, the smoothing constant must be close to

Customers arrive at a ticket counter at a rate of $$50$$ per hr and tickets are issued in the order of their arrival. The average time taken for issuing a ticket is $$1$$ $$min.$$ Assuming that customer arrivals form a Poisson process and service times are exponentially distributed, the average waiting time in queue in $$min$$ is

A linear programming problem is shown below.
$$\eqalign{ & Maximize\,\,\,\,3x + 7y \cr & Subject\,\,to\,\,\,3x + 7y \le 10 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4x + 6y \le 8 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,\,\,y \ge 0 \cr} $$

It has ..............

A bar is subjected to fluctuating tensile load from $$20$$ $$kN$$ to $$100$$ $$kN.$$ The material has yield strength of $$240$$ $$MPa$$ and endurance limit in reversed bending is $$160$$ $$MPa.$$ According to the Soderberg principle, the area of cross-section in $$m{m^2}$$ of the bar for a factor of safety of $$2$$ is

A single riveted lap joint of two similar plates as shown in the figure below has the following geometrical and material details.

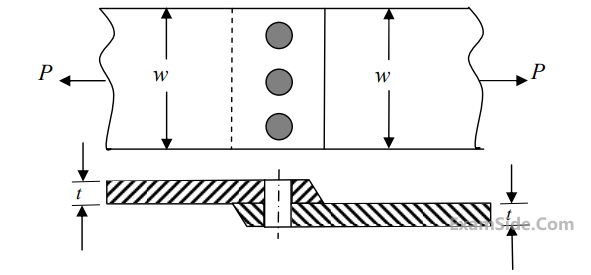
width of the plate $$w = 200$$ $$mm,$$ thickness of the plate $$t = 5$$ $$mm,$$ number of rivets $$n = 3,$$ diameter of the rivet $${d_r} = 10\,\,\,mm,$$ diameter of the rivet hole $${d_h} = 11\,\,\,mm,$$ allowable tensile stress of the plate $${\sigma _p} = 200\,\,MPa,$$ allowable shear stress of the rivet $${\sigma _s} = 100\,\,MPa$$ and allowable bearing stress of the rivet $${\sigma _c} = 150\,\,MPa.$$

If the rivets are to be designed to avoid crushing failure, the maximum permissible load $$P$$ in $$k/N$$ is

A single riveted lap joint of two similar plates as shown in the figure below has the following geometrical and material details.

width of the plate $$w = 200$$ $$mm,$$ thickness of the plate $$t = 5$$ $$mm,$$ number of rivets $$n = 3,$$ diameter of the rivet $${d_r} = 10\,\,\,mm,$$ diameter of the rivet hole $${d_h} = 11\,\,\,mm,$$ allowable tensile stress of the plate $${\sigma _p} = 200\,\,MPa,$$ allowable shear stress of the rivet $${\sigma _s} = 100\,\,MPa$$ and allowable bearing stress of the rivet $${\sigma _c} = 150\,\,MPa.$$

If the plates are to be designed to avoid tearing failure, the maximum permissible load $$P$$ in $$kN$$ is

A cube shaped casting solidifies in $$5$$ min. The solidification time in min for a cube of the same material, which is $$8$$ times heavier than the original casting, will be

In a rolling process, the state of stress of the material undergoing deformation is

In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$

The normal force acting at the chip-tool interface in $$N$$ is

Two cutting tools are being compared for a machining operation. The tool life equations are:
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,Carbi{\mathop{\rm de}\nolimits} \,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,V{T^{1.6}} = 3000 \cr & \,\,\,\,\,\,\,\,\,\,\,\,HSS\,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.6}} = 200 \cr} $$

Where $$V$$ is the cutting speed in $$m/min$$ and $$T$$ is the tool life in $$min.$$ The carbide tool will provide higher tool life if the cutting speed in $$m/min$$ exceeds

In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$

The orthogonal rake angle of the cutting tool in degrees is

A steel bar $$200$$ $$mm$$ in diameter is turned at a feed of $$0.25$$ $$mm/rev$$ with a depth of cut of $$4$$ $$mm.$$ The rotational speed of the work piece is $$160$$ $$rpm.$$ The material removal rate in $$m{m^3}/s$$ is

A metric thread of pitch $$2$$ $$mm$$ and thread angle 60° is inspected for its pitch diameter using 3-wire method. The diameter of the best size wire in mm is $${60^ \circ }$$ is inspected for its pitch diameter using $$3$$- wire method. The diameter of the best size wire in $$mm$$ is

Cylindrical pins of $${25^{\matrix{ { + 0.020} \cr { + 0.010} \cr } }}\,\,mm$$ diameter are electroplated in a shop. Thickness of the plating is $$30 \pm 0.2$$ micron. Neglecting gage tolerances, the size of the $$GO$$ gage in $$mm$$ to inspect the plated components is

In a $$CAD$$ package, mirror image of a $$2D$$ points $$P(5, 10)$$ is to be obtained about a line which passes through the origin and makes an angle of $${45^ \circ }$$ counterclockwise with the $$X$$-axis. The coordinates of the transformed points will be

A rod of length $$L$$ having uniform cross-sectional area $$A$$ is subjected to a tensile force $$P$$ as shown in the figure below. If the Young’s modulus of the material varies linearly from $${E_1}$$ to $${E_2}$$ along the length of the rod, the normal stress developed at the section $$-$$ $$SS$$ is

A simply supported beam of length $$L$$ is subjected to a varying distributed load $$\sin \left( {3\pi x/L} \right)N{m^{ - 1}},$$ where the distance $$x$$ is measured from the left support. The magnitude of the vertical reaction force in $$N$$ at the left support is

A long thin walled cylindrical shell, closed at both the ends, is subjected to an internal pressure. The ratio of the hoop stress (circumferential stress) to longitudinal stress developed in the shell is

For a ductile material, toughness is a measure of

Two threaded bolts A and B of same material and length are subjected to identical tensile load. If the elastic strain energy stored in bolt A is 4 times that of bolt B and the mean diameter of bolt A is 12 mm, the mean diameter of bolt B in mm is

A link OB is rotating with a constant angular velocity of 2 rad/s in counter clockwise direction and a block is sliding radially outward on it with an uniform velocity of 0.75 m/s with respect to the rod, as shown in the figure below. If OA = 1 m, the magnitude of the absolute acceleration of the block at location A in m/s² is

A planar closed kinematic chain is formed with rigid links $$PQ = 2.0 m, QR = 3.0 m, RS = 2.5 m$$ and $$SP = 2.7 m$$ with all revolute joints. The link to be fixed to obtain a double rocker (rocker-rocker) mechanism is

A compound gear train with gears P, Q, R and S has number of teeth 20, 40, 15 and 20, respectively. Gears Q and R are mounted on the same shaft as shown in the figure below. The diameter of the gear Q is twice that of the gear R. If the module of the gear R is 2 mm, the center distance in mm between gears P and S is

A flywheel connected to a punching machine has to supply energy of $$400$$ Nm while running at a mean angular speed of $$20$$ rad/s. If the total fluctuation of speed is not to exceed $$ \pm 20\% $$, the mass moment of inertia of the flywheel in kg-m² is

If two nodes are observed at a frequency of $$1800$$ rpm during whirling of a simply supported long slender rotating shaft, the first critical speed of the shaft in rpm is

A single degree of freedom system having mass $$1$$ $$kg$$ and stiffness $$10$$ $$kN/m$$ initially at rest is subjected to an impulse force of magnitude $$5$$ $$kN$$ for $${10^{ - 4}}$$ seconds. The amplitude in $$mm$$ of the resulting free vibration is

Specific enthalpy and velocity of steam at inlet and exit of a steam turbine, running under steady state, are as given below:

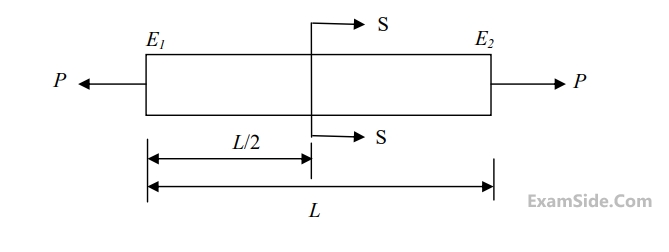
The rate of heat loss from the turbine per $$kg$$ of steam flow rate is $$5$$ $$kW.$$ Neglecting changes in potential energy of steam, the power developed in $$kW$$ by the steam turbine per $$kg$$ of steam flow rate, is

A cylinder contains $$5\,\,{m^3}$$ of an ideal gas at a pressure of $$1$$ bar. This gas is compressed in a reversible isothermal process till its pressure increases to $$5$$ bar. The work in $$kJ$$ required for this process is

The pressure, temperature and velocity of air flowing in a pipe are $$5$$ $$bar,$$ $$500$$ $$K$$ and $$50$$ $$m/s,$$ respectively. The specific heats of air at constant pressure and at constant volume are $$1.005kJ/kgK$$ and $$0.718$$ $$kJ/kgK,$$ respectively. Neglect potential energy. If the pressure and temperature of the surroundings are $$1$$ bar and $$300$$ $$K,$$ respectively, the available energy in $$kJ/kg$$ of the air stream is

In order to have maximum power from a Pelton turbine, the bucket speed must be